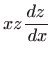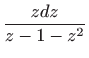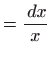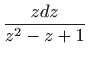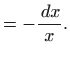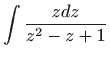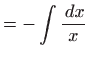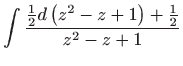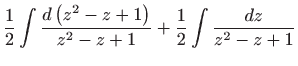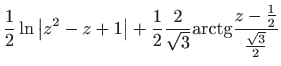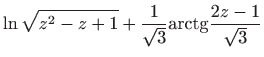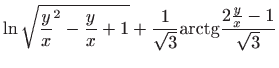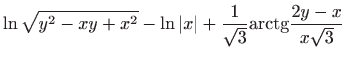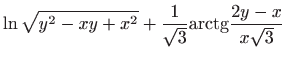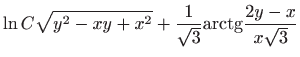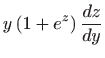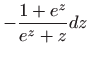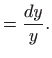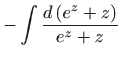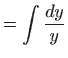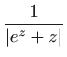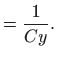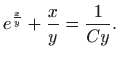☰
matematika2
Jednadžbe sa separiranim varijablama
DIFERENCIJALNE JEDNADŽBE
Diferencijalne jednadžbe koje se
Homogene diferencijalne jednadžbe
Odredite opće rješenje diferencijalnih jednadžbi
- a)
-
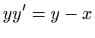 ,
,
- b)
-
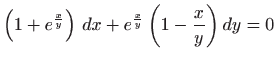 .
.
Rješenje.
- a)
- Uvrštavanjem
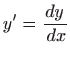 u
zadanu diferencijalnu jednadžbu dobivamo
u
zadanu diferencijalnu jednadžbu dobivamo
odnosno,
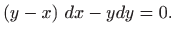 |
(5.2) |
Ovo je diferencijalna jednadžba prvog stupnja homogenosti pa je
rješavamo supstitucijom:
Uvrštavanjem u (5.2) dobivamo
Ovo je diferencijalna jednadžba separiranih varijabli, pa vrijedi
Vraćanjem susptitucije
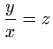 dobivamo
dobivamo
- b)
- Ovo je homogena diferencijalna jednadžba stupnja homogenosti
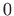 koju rješavamo supstitucijom:
koju rješavamo supstitucijom:
Uvrštavanjem u zadanu diferencijalnu jednadžbu dobivamo
Ovo je diferencijalna jednadžba sa separiranim varijablama pa vrijedi
Vraćanjem susptitucije
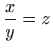 dobivamo
dobivamo
Jednadžbe sa separiranim varijablama
DIFERENCIJALNE JEDNADŽBE
Diferencijalne jednadžbe koje se
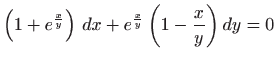 .
.
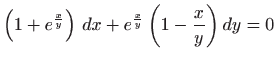 .
.
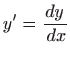 u
zadanu diferencijalnu jednadžbu dobivamo
u
zadanu diferencijalnu jednadžbu dobivamo