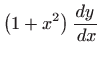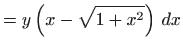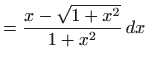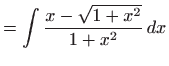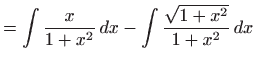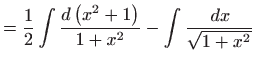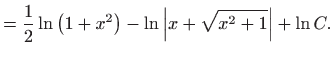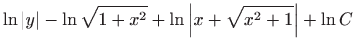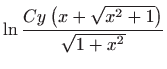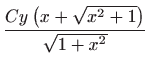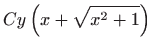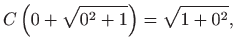☰
matematika2
Logistička jednadžba
DIFERENCIJALNE JEDNADŽBE
Homogene diferencijalne jednadžbe
Jednadžbe sa separiranim varijablama
- a)
- Odredite opće rješenje diferencijalne jednadžbe
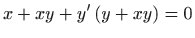 .
.
- b)
- Odredite opće rješenje diferencijalne jednadžbe
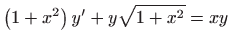 te
partikularno rješenje koje zadovoljava početni uvjet
te
partikularno rješenje koje zadovoljava početni uvjet
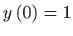 .
.
Rješenje.
- a)
- Uvrštavanjem
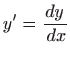 u
zadanu diferencijalnu jednadžbu dobivamo
u
zadanu diferencijalnu jednadžbu dobivamo
Ovo je diferencijalna jednadžba separiranih varijabli
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.2],
pa je rješavamo integriranjem:
[M2, poglavlje 5.2],
pa je rješavamo integriranjem:
Sređivanjem dobivamo
- b)
- Uvrštavanjem
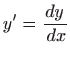 u
zadanu diferencijalnu jednadžbu dobivamo
u
zadanu diferencijalnu jednadžbu dobivamo
Vrijedi
Za početni uvjet
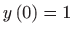 dobivamo
dobivamo
iz čega slijedi 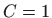 , odnosno, partikularno rješenje za ovaj početni uvjet je
, odnosno, partikularno rješenje za ovaj početni uvjet je
Logistička jednadžba
DIFERENCIJALNE JEDNADŽBE
Homogene diferencijalne jednadžbe
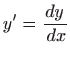 u
zadanu diferencijalnu jednadžbu dobivamo
u
zadanu diferencijalnu jednadžbu dobivamo
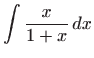
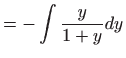
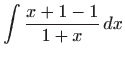
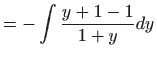
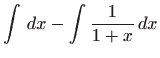
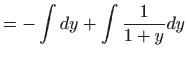
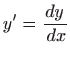 u
zadanu diferencijalnu jednadžbu dobivamo
u
zadanu diferencijalnu jednadžbu dobivamo