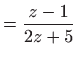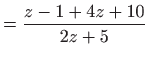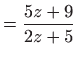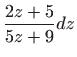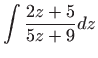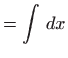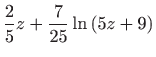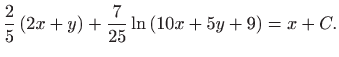☰
matematika2
Homogene diferencijalne jednadžbe
DIFERENCIJALNE JEDNADŽBE
Egzaktne diferencijalne jednadžbe i
Diferencijalne jednadžbe koje se svode na homogene
Odredite opće rješenje diferencijalnih jednadžbi
- a)
-
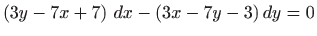 ,
,
- b)
-
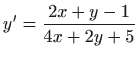 .
.
Rješenje.
- a)
- Zadanu diferencijalnu jednadžbu možemo pisati kao
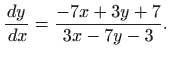 |
(5.3) |
Tražimo sjecište pravaca:
Rješavanjem sustava dobije se
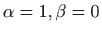 , pa zadanu diferencijalnu
jednadžbu rješavamo supstitucijom
, pa zadanu diferencijalnu
jednadžbu rješavamo supstitucijom
Uvrštavanjem u (5.3) dobivamo
Ovo je homogena diferencijalna jednadžba koju rješavamo
supstitucijom:
Uvrštavanjem u (5.4) dobivamo
Ovo je diferencijalna jednadžba sa separiranim varijablama pa je
rješavamo integriranjem
Sređivanjem dobivamo
Vraćanjem susptitucije
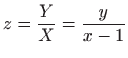 dobivamo
dobivamo
odnosno,
- b)
- Pravci
su paralelni
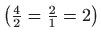 pa koristimo supstituciju
pa koristimo supstituciju
Uvrštavanjem u zadanu diferencijalnu jednadžbu dobivamo
Ovo je diferencijalna jednadžba sa separiranim varijablama pa vrijedi
Vraćanjem susptitucije
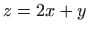 dobivamo
dobivamo
Homogene diferencijalne jednadžbe
DIFERENCIJALNE JEDNADŽBE
Egzaktne diferencijalne jednadžbe i
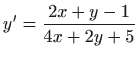 .
.
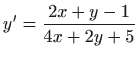 .
.
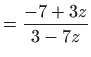
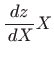
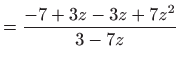
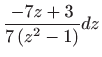
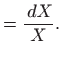
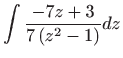
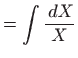
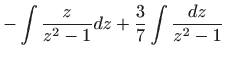
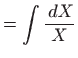
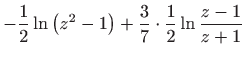
![$\displaystyle =\left[ \left( z^{2}-1\right) ^{-7}\left( \frac{z-1}{z+1}\right) ^{3}
\right] ^{\frac{1}{14}}$](img1755.gif)
![$\displaystyle =\left[ \left( z-1\right) ^{-4}\left( z+1\right) ^{-10}\right] ^{\frac{1
}{14}}$](img1756.gif)
![$\displaystyle =\left[ \left( z-1\right) ^{-2}\left( z+1\right) ^{-5}\right] ^{\frac{1
}{7}}.$](img1757.gif)
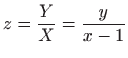 dobivamo
dobivamo
![$\displaystyle =\left[ \left( \frac{y}{x-1}-1\right) ^{-2}\left( \frac{
y}{x-1}+1\right) ^{-5}\right] ^{\frac{1}{7}},$](img1760.gif)