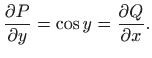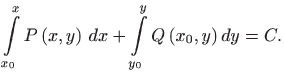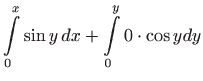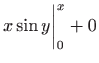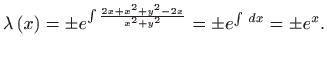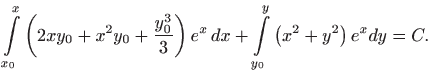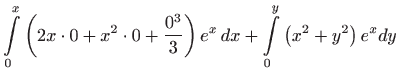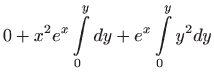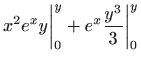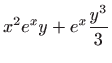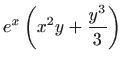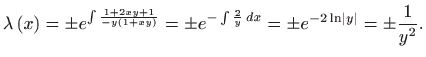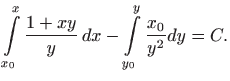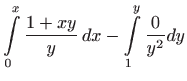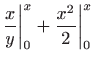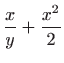☰
matematika2
Diferencijalne jednadžbe koje se
DIFERENCIJALNE JEDNADŽBE
Ortogonalne trajektorije
Egzaktne diferencijalne jednadžbe i integrirajući faktor
- a)
- Odredite opće rješenje diferencijalne jednadžbe
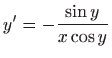 .
.
- b)
- Rješite diferencijalnu jednadžbu
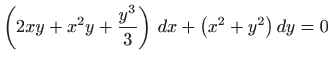 ,
ako je
,
ako je
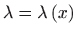 .
.
- c)
- Rješite diferencijalnu jednadžbu
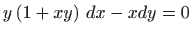 , ako je
, ako je
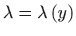 .
.
Rješenje.
- a)
- Zadanu diferencijalnu jednadžbu možemo zapisati u obliku
Ovo je egzaktna diferencijalna jednadžba
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.7], jer vrijedi
[M2, poglavlje 5.7], jer vrijedi
Rješenje zadane diferencijalne jednadžbe dobije se rješavanjem integrala
Za početnu točku
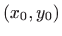 (uzmimo, na primjer, točku
(uzmimo, na primjer, točku
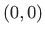 )
vrijedi
)
vrijedi
i to je rješenje zadane diferencijalne jednadžbe.
- b)
- Kako je
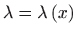 , koristimo
formule za inetgrirajući faktor
, koristimo
formule za inetgrirajući faktor
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.7]. Vrijedi
[M2, poglavlje 5.7]. Vrijedi
Rješenje dobivamo inetgriranjem:
Na primjer, za početnu točku
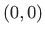 je
je
- c)
- Kako je
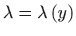 , koristimo
formule za inetgrirajući faktor
, koristimo
formule za inetgrirajući faktor
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.7], pa je
[M2, poglavlje 5.7], pa je
Rješenje dobivamo integriranjem
Na primjer, za početnu točku
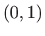 je
je
Diferencijalne jednadžbe koje se
DIFERENCIJALNE JEDNADŽBE
Ortogonalne trajektorije
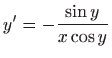 .
.
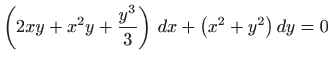 ,
ako je
,
ako je
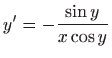 .
.
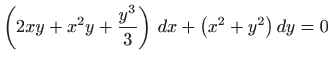 ,
ako je
,
ako je