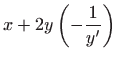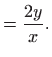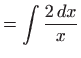☰
matematika2
Egzaktne diferencijalne jednadžbe i
DIFERENCIJALNE JEDNADŽBE
Singularna rješenja
Ortogonalne trajektorije
Odredite ortogonalne trajektorije familije elipsa
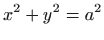 .
.
Rješenje.
Derivirajnem dobivamo
Diferencijalna jednadžba ortogonalnih trajektorija zadane familije elipsa
dobije se uvrštavanjem
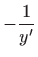 umjesto
umjesto
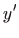 :
:
Ovo je diferencijalna jednadžba sa separiranim varijablama
pa vrijedi
Dakle, rješenje je familija parabola 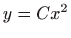 .
.
Egzaktne diferencijalne jednadžbe i
DIFERENCIJALNE JEDNADŽBE
Singularna rješenja
![]() .
.
![]() umjesto
umjesto
![]() :
: