☰
matematika2
Ortogonalne trajektorije
DIFERENCIJALNE JEDNADŽBE
Linearne diferencijalne jednadžbe prvog
Singularna rješenja
Odredite singularna rješenja diferencijalnih jednadžbi
- a)
-
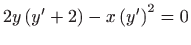 ,
,
- b)
-
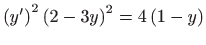 .
.
Rješenje.
- a)
- Deriviranjem zadane diferencijalne jednadžbe po
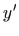 dobivamo
dobivamo
Da bi dobili potencijalna singularna rješenja zadane diferencijalne jednadžbe rješavamo sustav:
Iz druge jednadžbe slijedi
pa uvrštavanjem u prvu dobivamo
Rješenja ove jednadžbe su
Da bi to bila singularna rješenja zadane diferencijalne jednadžbe
nužno je i dovoljno je da je zadovoljavaju, pa ćemo to i provjeriti:
za
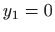 je
je
pa
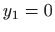 jest singularno rješenje.
Za
jest singularno rješenje.
Za
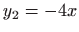 je
je
pa je i
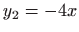 singularno rješenje zadane diferencijalne jednadžbe.
singularno rješenje zadane diferencijalne jednadžbe.
- b)
- Deriviranjem zadane diferencijalne jednadžbe po
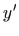 dobivamo
dobivamo
Rješimo sustav:
Iz prve jednadžbe slijedi
pa uvrštavanjem u drugu dobivamo
Rješenja ove jednadžbe su
Provjerimo zadovoljavaju li ova rješenja početnu diferencijalnu
jednadžbu: za
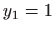 je
je
pa
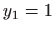 jest singularno rješenje.
Za
jest singularno rješenje.
Za
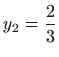 je
je
pa
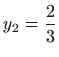 nije singularno rješenje zadane diferencijalne jednadžbe.
nije singularno rješenje zadane diferencijalne jednadžbe.
Ortogonalne trajektorije
DIFERENCIJALNE JEDNADŽBE
Linearne diferencijalne jednadžbe prvog
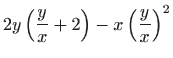
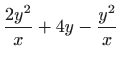
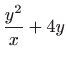
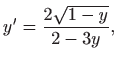
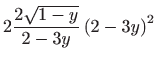
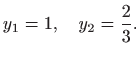
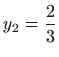 je
je
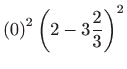
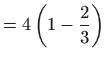
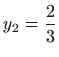 nije singularno rješenje zadane diferencijalne jednadžbe.
nije singularno rješenje zadane diferencijalne jednadžbe.