☰
matematika2
Linearne diferencijalne jednadžbe prvog
DIFERENCIJALNE JEDNADŽBE
Eulerova metoda
Bernoullijeva diferencijalna jednadžba
Odredite opće rješenje diferencijalnih jednadžbi:
- a)
-
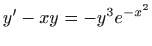 ,
,
- b)
-
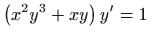 .
.
Rješenje.
- a)
- Uvođenjem supstitucije
i dijeljenjem zadane diferencijalne jednadžbe s
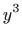 dobivamo
dobivamo
što je linearna diferencijalna jednadžba.
U formulu za rješavanje linearne diferencijalne jednadžbe
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.8] uvrstimo
[M2, poglavlje 5.8] uvrstimo
i dobijemo
Vraćanjem susptitucije
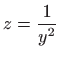 dobivamo
dobivamo
- b)
- Neka je
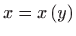 . Tada je
. Tada je
pa zadanu diferencijlanu jednadžbu možemo pisati kao:
Dijeljenjem zadane diferencijalne jednadžbe s
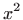 dobivamo
dobivamo
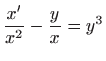 |
(5.6) |
pa uvodimo supstituciju
Sada diferencijalna jednadžba (5.6) glasi
To je linearna diferencijalna jednadžba u kojoj je
pa uvrštavanjem u formulu za rješavanje linearne diferencijalne jednadžbe
![[*]](../icons.gif/crossref.gif) [M2, poglavlje 5.8] dobivamo
[M2, poglavlje 5.8] dobivamo
Rješavanjem integrala i vraćanjem supstitucije dobivamo
konačno rješenje zadane diferencijalne jednadžbe:
Linearne diferencijalne jednadžbe prvog
DIFERENCIJALNE JEDNADŽBE
Eulerova metoda
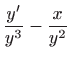
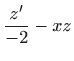
![$\displaystyle =e^{-\int 2x dx}\left[ \int 2e^{-x^{2}}e^{\int 2x dx} dx+C\right]$](img1930.gif)
![$\displaystyle =e^{-x^{2}}\left[ \int 2e^{-x^{2}}e^{x^{2}} dx+C\right]$](img1931.gif)
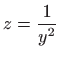 dobivamo
dobivamo
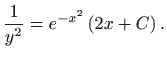
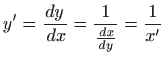
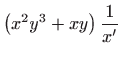
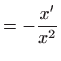
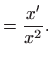
![$\displaystyle z=e^{-\int ydy}\left[ -\int y^{3}e^{\int ydy}dy+C\right].$](img1947.gif)