×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Problem najmanjih kvadrata     Problem najmanjih kvadrata     Metoda najmanjih kvadrata

Linearna regresija

Linearnu regresiju ćemo najbolje objasniti na primjeru. Neka je zadano pet točaka u ravnini

$$\begin{tabular}{r\vert lllll} x& 1 & 3 & 4 & 6 & 7 \hline y& 1 & 3 & 2 & 4 & 3 \end{tabular}$$

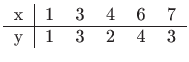
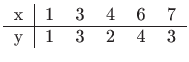
kao na slici 6.1.

Slika: Pet točaka u ravnini

Ukoliko bi pravac $y=kx+l$ prolazio kroz sve zadane točke, onda bi za svaku točku $(x_1,y_i)$ , $i=1,2,\ldots, 5$ vrijedilo

$$k x_i+l=y_i.$$

U našem slučaju to daje sustav linearnih jednadžbi

$$k+l =1$$

$$3k+l =3$$

$$4k+l =2$$

$$6k+l =4$$

$$7k+l =3.$$

Ovo je sustav s pet jednadžbi i dvije nepoznanice $k$ i $l$ . Matrični zapis sustava glasi (vidi M1, poglavlje 2.2)

$$\begin{bmatrix}1 & 1 3 & 1 4 & 1 6 & 1 7 & 1 \end{bmatrix... ...atrix}k l \end{bmatrix}= \begin{bmatrix}1 3 2 4 3 \end{bmatrix},$$

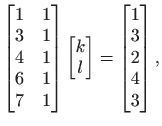
odnosno $A\mathbf{x}=\mathbf{b}$ gdje je

$$A=\begin{bmatrix}1 & 1 3 & 1 4 & 1 6 & 1 7 & 1 \end{bmatr... ...ad \mathbf{b}=\mathbf{y}= \begin{bmatrix}1 3 2 4 3 \end{bmatrix}.$$

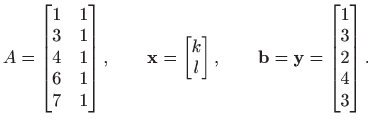
Ne postoji pravac koji prolazi kroz zadane točke pa zadani sustav očito nije rješiv i postavlja se pitanje što možemo napraviti. Ako bi sustav bio rješiv, onda bi vrijedilo $A\mathbf{x} - \mathbf{b}=0$ odnosno $\Vert A\mathbf{x} - \mathbf{b}\Vert=0$ pa je prirodan zahtjev da izraz $A\mathbf{x} - \mathbf{b}$ bude što bliži nul-stupcu, odnosno da norma $\Vert A\mathbf{x} - \mathbf{b}\Vert$ bude što manja moguća. Taj zahtjev matematički zapisujemo kao

$$\Vert A\mathbf{x} - \mathbf{b}\Vert \to \min.$$

Ako je $x$ rješenje ovog problema, onda je $x$ također i rješenje problema

$$\Vert A\mathbf{x} - \mathbf{b}\Vert^2 \to \min$$

pa naziv problem najmanjih kvadrata slijedi iz definicije norme vektora.

Postupak za rješavanje problema najmanjih kvadrata je u ovom slučaju jednostavan: rješenje $\mathbf{x}$ dobit ćemo kao rješenje sustava od dvije jednadžbe i dvije nepoznanice^6.1

$$A^T A \mathbf{x}=A^T \mathbf{b}.$$

Vrijedi

$$A^TA=\begin{bmatrix}111 & 21 21 & 5 \end{bmatrix}, \qquad A^T \mathbf{b}= \begin{bmatrix}63 13 \end{bmatrix}$$

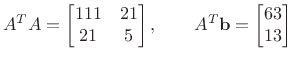
pa rješenje $x$ dobijemo kao rješenje sustava

$$\begin{bmatrix}111 & 21 21 & 5 \end{bmatrix} \begin{bmatrix}k l \end{bmatrix} = \begin{bmatrix}63 13 \end{bmatrix}.$$

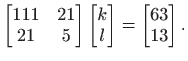
Ovaj sustav možemo lako riješiti Gaussovom eliminacijom (vidi M1, poglavlje 2.4) ili, još jednostavnije, Cramerovim pravilom (vidi M1, poglavlje 2.9.5):

$$k=\frac{\begin{vmatrix}63 & 21 13 & 5 \end{vmatrix}}{\begin{vm... ...nd{vmatrix}}{\begin{vmatrix}111 & 21 21 & 5 \end{vmatrix}}=\frac{120}{114}.$$

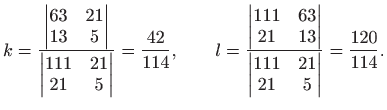
Geometrijska interpretacija rješenja je sljedeća (vidi sliku 6.2): pravac $y=kx+l$ "najbolje" prolazi točkama $(x_i,y_i)$ , $i=1,2,\ldots, 5$ u smislu da je suma kvadrata udaljenosti između zadanih točaka $(x_i,y_i)$ i točaka na pravcu $(x_i,kx_i+l)$ minimalna. Drugim riječima,

$$\sum_{i=1}^5 [y_i - (kx_i+l)]^2 \to \min.$$

Slika: Rješenje problema najmanjih kvadrata

Napomena 6.1   Ravninski problem najmanjih kvadrata zove se linearna regresija, a pravac $y=kx+l$ zove se regresijski pravac.

Rješenje prethodnog problem i slike 6.1 i 6.2 mogu se dobiti pomoću sljedećeg Matlab (Octave) programa

Octave On-line

x=[1 3 4 6 7] y=[1 3 2 4 3] plot(x,y,'b*') A=[x' ones(5,1)] b=y' xLS=(A'*A)\(A'*b) k=xLS(1) l=xLS(2) yLS=k*x+l plot(x,y,'b*',x,yLS,'r')

     

[Octave On-line Home]    [Octave User's Guide]

U Matlabovoj sintaksi A' je transponirana matrica matrice $A$ , ones(5,1) je vektor dimenzije $5\times 1$ sa svim elementima jednakim $1$ , dok izraz oblika x=A\b daje rješenje sustava $Ax=b$ . Štoviše, u slučaju preodređenog sustava kao u našem primjeru, Matlabova naredba xLS=A\b automatski daje rješenje problema najmanjih kvadrata. Zamijenite liniju xLS=(A'*A)\(A'*b) s xLS=A\b i uvjerite se da su rješenja ista!

Zadatak 6.1   Kroz točke

$$\begin{tabular}{r\vert lllll} x & -1 & 1 & 2 & 3 & 5 \hline y & 1 & 0 & 1 & 2 & 3 \end{tabular}$$

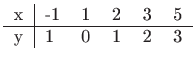
provucite najbolji pravac u smislu najmanjih kvadrata. Nacrtajte zadane točke i dobiveni pravac te provjerite rješenje pomoću Matlaba ili programa Octave On-line.

Zadatak 6.2   Prema podacima Državnog zavoda za statistiku^6.2 prosječna neto plaća u siječnju navedenih godina bila je sljedeća:

$$\begin{tabular}{r\vert lllllll} siječanj & 2007& 2008& 2009& 20... ...e plaća (kn) & 4.739& 5.019& 5.307& 5.258& 5.342& 5.463& 5.529 \end{tabular}.$$

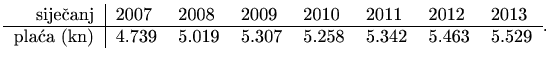
Izračunajte i nacrtajte regresijski pravac, predvidite neto plaću za siječanj 2018. i usporedite sa stvarnim iznosom. Za računanje možete koristiti Matlab ili program Octave On-line.

Problem najmanjih kvadrata     Problem najmanjih kvadrata     Metoda najmanjih kvadrata