Za formiranje Householderove matrice ![]() potrebno je
potrebno je
![]() računskih operacija. Za množenje nekog vektora
računskih operacija. Za množenje nekog vektora ![]() Householderovom matricom također je potrebno
Householderovom matricom također je potrebno ![]() računskih operacija.
No, umnožak
računskih operacija.
No, umnožak
![]() može se izračunati bez formiranja
matrice
može se izračunati bez formiranja
matrice ![]() :
:
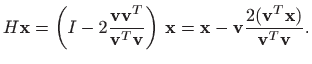
Za računanje produkta
Koristeći prethodna poboljšanja možemo napisati funkcije za
računanje QR rastava.
Prva funkcija računa vektor
![]() iz zadanog
vektora
iz zadanog
vektora
![]() prema formuli (6.4) i napomeni 6.3:
prema formuli (6.4) i napomeni 6.3:
function v=House(x)
% računa Householderov vektor v iz vektora x
sig=sign(x(1)); if sig==0, sig=1; end
v=x
v(1)=v(1)+sig*norm(v)
end
Slijedeća funkcija računa umnožak
function B=mnoziHouse(v,A)
% računa produkt HA=(I-2*v*v'/(v'*v))*A
% bez formiranja matrice H
beta=-2/(v'*v)
w=beta*A'*v
B=A+v*w'
end
Konačno, sljedeća funkcija računa QR rastav matrice
function [Q,R]=mojQR(A)
% QR rastav A=Q*R. A je m x n i mora biti rank(A)=n.
[m,n]=size(A)
Q=eye(m)
for i=1:min(m-1,n)
v=House(A(i:m,i))
A(i:m,i:n)=mnoziHouse(v, A(i:m,i:n))
Q(i:m,:)=mnoziHouse(v, Q(i:m,:))
end
R=A
Q=Q'
end
[Q,R]=qr(A).
Octave On-line[Octave On-line Home] [Octave User's Guide] |