Koristeći svojstvo ortogonalne matrice ![]() da je
da je
![]() možemo lako riješiti problem najmanjih kvadrata.
Neka je
možemo lako riješiti problem najmanjih kvadrata.
Neka je ![]() matrica tipa
matrica tipa ![]() ,
, ![]() , neka je
, neka je
![]() i
neka je
i
neka je ![]() rastav matrice
rastav matrice ![]() .
Tada je
.
Tada je
Matricu
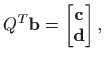
gdje je
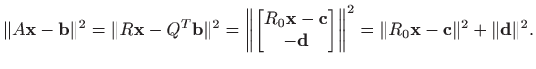
Kako je
Sljedeća funkcija rješava problem najmanjih kvadrata pomoću QR rastava:
function x=mojLS(A,b)
% Rješava problem najmanjih kvadrata || A*x - b || --> min
% za matricu punog stupčanog ranga A koristeći QR rastav.
[m,n]=size(A)
[Q,R]=mojQR(A)
b1=Q'*b
c=b1(1:n)
x=R(1:n,1:n)\c
end
x=A\b.
Octave On-line[Octave On-line Home] [Octave User's Guide] |