×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Binomni integral     NEODREĐENI INTEGRAL     Slobodan pad uz otpor

Integriranje reda funkcija

Konvergentan red funkcija može se, uz određene uvjete, derivirati član po član (vidi M1, poglavlje 6.4.3) . Slična je situacija i s integriranjem. Najvažnija primjena integriranja reda funkcija je računanje integrala funkcija koje nisu elementarno integrabilne. Druga primjena je razvijanje u red potencija onih funkcija kod kojih se to ne može direktno napraviti pomoću Taylorove formule (vidi M1, poglavlje 6.5).

U sljedećem teoremu koriste se pojmovi uniformne konvergencije reda funkcija (vidi M1, poglavlje 6.4) i reda potencija (vidi M1, poglavlje 6.4.2).

Teorem 1.9   Neka red neprekidnih funkcija $\sum\limits_{i=1}^{\infty} f_n(x)$ konvergira uniformno prema funkciji $s(x)$ na intervalu $I$ , odnosno

$$s(x)=\sum_{i=1}^{\infty} f_n(x), \qquad \forall x\in I.$$

Tada za svaki $x\in I$ vrijedi

$$\int s(x) dx=\sum_{i=1}^{\infty} \int f_n(x) dx.$$

Za red potencija posebno vrijedi

$$\int \big( \sum_{n=0}^{\infty} a_n(x-x_0)^n \big) dx = \sum_{n=0}^{\infty} \frac{a_n}{n+1}(x-x_0)^{n+1} +C$$

na intervalu konvergencije reda $\sum_{n=0}^{\infty} a_n(x-x_0)^n$ .

Pokažimo kako pomoću teorema 1.9 možemo izračunati razvoj u red potencija integrala koji nisu elementarno rješivi.

Primjer 1.14  

a)

Integral

$$I = \int e^{-x^2} dx$$

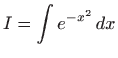
nije elementarno rješiv, odnosno rješenje nije elementarna funkcija i ne može se prikazati konačnim brojem zbrajanja, oduzimanja, množenja, dijeljenja i komponiranja elementarnih funkcija. Ovaj integral je od velike važnosti u teoriji vjerojatnosti i statistici jer funkcija vjerojatnosti Gaussove ili normalne razdiobe ima oblik funkcije $f(x)=e^{-x^2}$ .

Maclaurinov razvoj funkcije $e^x$ glasi (vidi M1, poglavlje 6.5)

$$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\cdots =\sum_{n=0}^{\infty}\frac{x^n}{n!}, \quad \forall x\in \mathbb{R}.$$

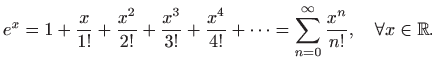
Pri tome je konvergencija uniformna (vidi M1, teorem 6.16). Zamijenimo li $x$ s $-x^2$ , za svaki $x\in\mathbb{R}$ vrijedi

$$e^{-x^2}=1-\frac{x^2}{1!}+\frac{x^4}{2!}-\frac{x^6}{3!}+\cdots = \sum_{n=0}^{\infty}\frac{(-1)^n x^{2n}}{n!},$$

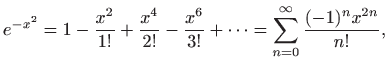
pri čemu je konvergencija uniformna. Teorem 1.9 daje

$$I=\int e^{-x^2} dx= \sum_{n=0}^{\infty}\frac{(-1)^n}{n!} \int x^{2n} dx= \sum_{n=0}^{\infty}\frac{(-1)^n}{n!} \cdot \frac{x^{2n+1}}{2n+1} +C.$$

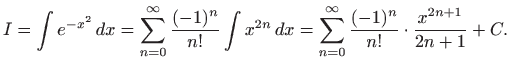
Dakle, našli smo razvoj traženog integrala u uniformno konvergentan red potencija. Pomoću ovog reda možemo izračunati vrijednost funkcije $I=I(x)$ u bilo kojoj točki $x$ sa željenom točnošću. Dobiveni red nije Taylorov red, tako da ne vrijedi formula za ostatak. Međutim, kako je red alterniran, zaključujemo da pogreška prilikom aproksimacije konačnom parcijalnom sumom nije veća od prvog zanemarenog člana. Na primjer, vrijednost integrala $I$ u točki $x=0.1$ uz $C=0$ izračunana pomoću prva tri člana reda (za $n=0,1,2$ ) je

$$I(0.1)=\frac{0.1}{1}-\frac{0.1^3}{3}+\frac{1}{2}\cdot \frac{0.1^5}{5} = 0.099667\dot 6.$$

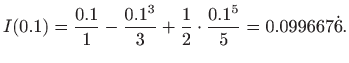
Četvrti član reda (za $n=3$ ) jednak je

$$-\frac{1}{6}\cdot \frac{0.1^7}{7}=-2.3809\cdot 10^{-9},$$

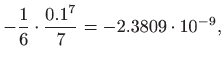
pa zaključujemo da pogreška nije veća od $2.3809\cdot 10^{-9}$ , odnosno

$$I(0.1) \in [0.099667\dot 6-2.3809\cdot 10^{-9}, 0.099667\dot 6]$$

$$=[0.099667664, 0.099667667],$$

što je relativna pogreška manja od tri stota dijela tisućitog dijela jednog promila.

b)

Integral

$$I=\int \frac{\sin x}{x} dx$$

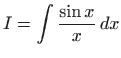
također nije elementarno rješiv. Maclaurinov razvoj funkcije $\sin x$ glasi (vidi M1, poglavlje 6.5)

$$\sin x = \frac{x}{1!}-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!... ...n=0}^{\infty}(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}, \quad \forall x\in \mathbb{R},$$

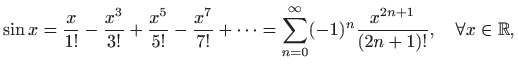
pri čemu je konvergencija uniformna. Za $x\neq 0$ vrijedi

$$\frac{\sin x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+ \cdots = \sum_{n=0}^{\infty}(-1)^{n}\frac{x^{2n}}{(2n+1)!}.$$

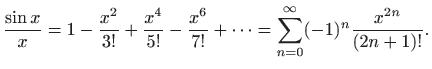
Primijetimo da je red na desnoj strani definiran za svaki $x\in R$ , dok zadana funkcija nije definirana u točki $x=0$ . No, kako se oni razlikuju samo u jednoj točki po definiciji 1.1 oni imaju istu primitivnu funkciju, pa tako i isti integral. Sada možemo primijeniti teorem 1.9:

$$I=\int \frac{\sin x}{x} dx= \sum_{n=0}^{\infty}\frac{(-1)^n}{(2... ... dx= \sum_{n=0}^{\infty}\frac{(-1)^n}{(2n+1)!} \cdot \frac{x^{2n+1}}{2n+1} +C.$$

Zadatak 1.10  

a)

Pomoću razvoja u red potencija izračunajte integral

$$\int \frac{e^{-x}}{x} dx.$$

b)

Izračunajte vrijednosti integrala iz primjera 1.14 a) u točkama $x=0.2$ i $x=1$ uz $C=0$ koristeći prva tri člana reda i ocijenite pogrešku.

c)

$k$ -tu parcijalnu sumu reda $I$ iz primjera 1.14 a) u točki $x$ uz $C=0$ možemo izračunati pomoću sljedećeg Matlab programa:

Octave On-line

format long k=3; x=0.1; I=0; for n=1:k I=I+(-1)^(n-1)*x^(2*n-1)/((2*n-1)*prod(1:n-1)); end I pogreska=(-1)^k*x^(2*k+1)/((2*k+1)*prod(1:k)) relativna_pogreska=abs(pogreska/I)

     

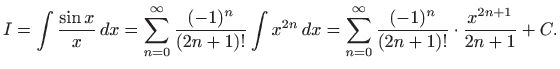
[Octave On-line Home]    [Octave User's Guide]

Izračunajte aproksimacije vrijednosti integrala $I$ u različitim točkama $x$ s različitim parcijalnim sumama (za različite vrijednosti $k$ ), te odgovarajuće pogreške. Naredba format long je potrebna da bi se prikazalo svih 16 znamenki koje program računa.

d)

Preradite prethodni program tako da računa $k$ -tu parcijalnu sumu integrala $I$ iz primjera 1.14b te izračunajte vrijednosti integrala i odgovarajuće pogreške u raznim točkama $x$ za razne vrijednosti $k$ .

e)

Funkciju $e^{-x^2}$ možemo nacrtati na intervalu $[-4,4]$ pomoću sljedećeg Matlab programa:

  x=-4:0.01:4;
  plot(x,exp(-x.^2))

Nacrtajte funkciju na različitim intervalima koristeći program Octave On-line.

Teorem 1.9 također možemo iskoristiti za računanje razvoja u red potencija onih funkcija kod kojih to ne možemo direktno napraviti.

Primjer 1.15   Funkciju $\mathop{\mathrm{arctg}}\nolimits x$ ne možemo razviti u red potencija direktnom primjenom Taylorove formule (vidi M1, poglavlje 6.5). Naime, sukcesivno deriviranje daje

$$(\mathop{\mathrm{arctg}}\nolimits x)'=\frac{1}{1+x^2}, \qquad (\mathop{\mathrm{arctg}}\nolimits x)''=\frac{-1}{(1+x^2)^2} \cdot 2x, \ldots$$

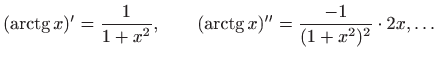
pa derivacije postaju vrlo složene. Zato ćemo koristiti geometrijski red (vidi M1, poglavlje 6.4) za koji vrijedi

$$1+x+x^2+x^3+x^4+\cdots =\frac{1}{1-x},\qquad \forall x\in(-1,1).$$

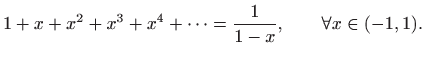
Zamijenimo li $x$ s $-x^2$ , za $x\in (-1,1)$ vrijedi

$$1-x^2+x^4-x^6+\cdots =\sum_{n=0}^{\infty} (-1)^n x^{2n} = \frac{1}{1-(-x^2)}=\frac{1}{1+x^2}=(\mathop{\mathrm{arctg}}\nolimits x)'.$$

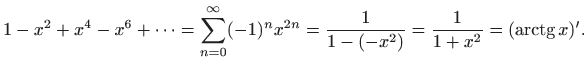
Teorem 1.9 daje

$$\mathop{\mathrm{arctg}}\nolimits x =\sum_{n=0}^{\infty} (-1)^n\int x^{2n} dx= \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{2n+1} +C.$$

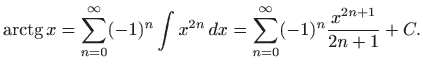
Na lijevoj strani jednakosti nalazi se konkretna funkcija pa konstanta $C$ ne može biti proizvoljna. Iz uvjeta $\mathop{\mathrm{arctg}}\nolimits 0=0$ slijedi $C=0$ . Dakle,

$$\mathop{\mathrm{arctg}}\nolimits x =\sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{2n+1}, \qquad \forall x\in(-1,1).$$ (1.8)

Ispitajmo konvergenciju reda na desnoj strani u rubovima intervala. U točki $x=-1$ red glasi

$$\sum_{n=0}^{\infty} \frac{(-1)^{3n+1}}{2n+1}=-1+\frac{1}{3}-\frac{1}{5}+\cdots.$$

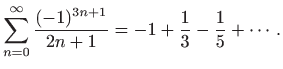
Ovaj red konvergira po Leibnitzovom kriteriju (vidi M1, poglavlje 6.2.4). Nadalje, zbog neprekidnosti lijeve i desne u jednakosti (1.8), zaključujemo da red konvergira prema $\mathop{\mathrm{arctg}}\nolimits (-1)=-\pi/4$ . Slično razmatranje za točku $x=1$ daje

$$\sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\cdots=\frac{\pi}{4}.$$

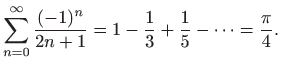
Gornji red možemo koristiti za računanje broja $\pi$ , međutim konvergencija je vrlo spora. Naime, red je alterniran pa zaključujemo da apsolutna vrijednost pogreške prilikom aproksimacije konačnom parcijalnom sumom nije veća od apsolutne vrijednosti prvog zanemarenog člana (slično smo već zaključili u primjeru 1.14a). Na primjer, kada zbrojimo prvih $1000$ članova reda, apsolutna vrijednost pogreške je manja od $\frac{1}{2001}$ , što znači da smo izračunali tek prve tri decimale broja $\pi$ .

Zadatak 1.11   $k$ -tu parcijalnu sumu prethodnog reda $I$ i odgovarajuću aproksimaciju broja $\pi$ možemo izračunati pomoću sljedećeg Matlab programa:

Octave On-line

format long k=1000; a=ones(k,1); a(2:2:k)=-1; for i=1:k; a(i)=a(i)/(2*i-1); end p=4*sum(a) pi

     

[Octave On-line Home]    [Octave User's Guide]

Izračunajte aproksimacije broja $\pi$ za različite vrijednosti $k$ i usporedite s pravom vrijednošću. Koliko se točnih decimala dobije za $n=10, 100, 1000$ ?

Binomni integral     NEODREĐENI INTEGRAL     Slobodan pad uz otpor