Kod trapezne formule odaberemo dekompoziciju
![]() koja dijeli interval
koja dijeli interval
![]() na
na ![]() jednakih dijelova,
jednakih dijelova,
pa je prirast jednak
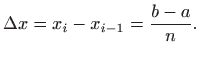
Zadanu krivulju
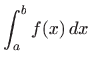 aproksimiramo s tako dobivenom integralnom sumom
aproksimiramo s tako dobivenom integralnom sumom
Vidimo da je integralna suma zapravo suma površina dobivenih trapeza,
pa odatle i ime trapezna formula. Površinu ![]() -tog trapeza računamo kao
zbroj površine pravokutnika i površine trokuta, što daje
-tog trapeza računamo kao
zbroj površine pravokutnika i površine trokuta, što daje
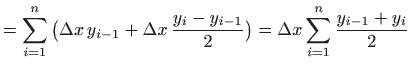 |
||
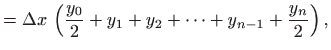 |
Pogrešku trapezne formule daje sljedeći teorem.
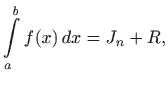
pri čemu je
![$\displaystyle \vert R\vert\leq M \frac{b-a}{12} \Delta x^2,\qquad M=\max_{x\in[a,b]}
\vert f''(x)\vert.
$](img1129.gif)
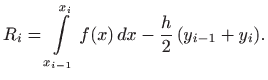
Promotrimo
![$\displaystyle R_i(h)=\int\limits _{x_{i-1}}^{x_{i-1}+h} f(x) dx-
\frac{h}{2} [f(x_{i-1})+f(x_{i-1}+h)].
$](img1133.gif)
Koristeći pravilo o deriviranju složene funkcije imamo
![$\displaystyle =f(x_{i-1}+h) -\displaystyle \frac{1}{2} [f(x_{i-1})+f(x_{i-1}+h)]-\displaystyle \frac{h}{2} f'(x_{i-1}+h)$](img1135.gif) |
||
![$\displaystyle =\displaystyle \frac{1}{2} [f(x_{i-1}+h) - f(x_{i-1})] - \displaystyle \frac{h}{2} f'(x_{i-1}+h),$](img1136.gif) |
||
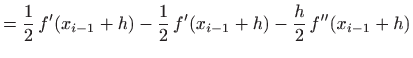 |
||
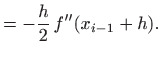 |
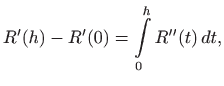
odnosno
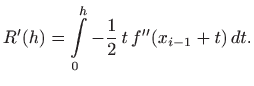
Teorem o srednjoj vrijednosti 2.4 primijenjen na funkcije
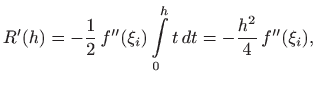
za neki
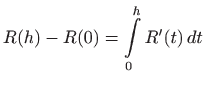
pa je
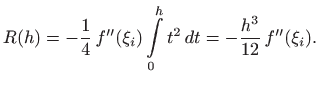
Dakle,
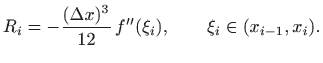
Konačno,
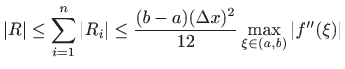
i teorem je dokazan.

Dakle,
Traženje broja ![]() u gornjoj formuli za ocjenu ostatka (pogreške)
je složeno. Računanjem druge derivacije zadane funkcije može se pokazati da je
u gornjoj formuli za ocjenu ostatka (pogreške)
je složeno. Računanjem druge derivacije zadane funkcije može se pokazati da je
![]() pa formula za ocjenu pogreške iz teorema 2.6 daje
pa formula za ocjenu pogreške iz teorema 2.6 daje
![]() . No, umjesto toga pogrešku možemo jednostavnije ocijeniti Richardsonovom
ekstrapolacijom (poglavlje 2.7.4).
. No, umjesto toga pogrešku možemo jednostavnije ocijeniti Richardsonovom
ekstrapolacijom (poglavlje 2.7.4).