Simpsonovu formulu
dobijemo ako umjesto linearnih koristimo
kvadratne aproksimacije zadane funkcije.
Preciznije, zadani interval ![]() podijelimo na paran
broj točaka
podijelimo na paran
broj točaka ![]() , uzmemo
, uzmemo
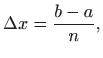
a zadanu funkciju
Određeni integral parabole ![]() na intervalu
na intervalu
![]() jednak je
jednak je
pa uvjeti da
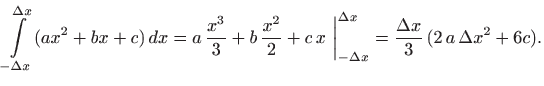
No, formule (2.13) povlače
pa je formula (2.12) dokazana.
Konačno, zbrajanjem integrala (2.12) za
![]() , nakon
sređivanja dobijemo Simpsonovu formulu
, nakon
sređivanja dobijemo Simpsonovu formulu
Pogrešku Simpsonove formule
daje sljedeći teorem2.3:
ako je četvrta derivacija ![]() neprekidna i omeđena na
intervalu
neprekidna i omeđena na
intervalu ![]() , onda vrijedi
, onda vrijedi
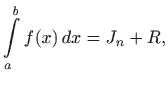
pri čemu za ostatak
![$\displaystyle \vert R\vert\leq M \frac{b-a}{180} \Delta x^4,\qquad M=\max_{x\in[a,b]}
\vert f^{IV}(x)\vert.
$](img1179.gif)