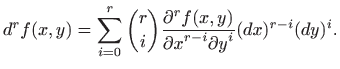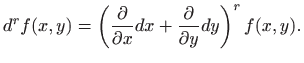Primjer 3.14 Neka je
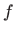
funkcija dviju varijabla.
Pod pretpostavkom da
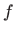
u nekoj okolini
točke
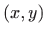
ima neprekidne
sve parcijalne derivacije
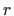
-tog reda, uvažavajući Schwarzov teorem,
za
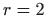
imamo
a za
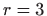
imamo
Nije teško dokazati (na primjer indukcijom) da za bilo koji
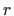
vrijedi
Zbog očigledne analogije s binomnom formulom gornji izraz često
skraćeno zapisujemo kao