×   HOME PREDAVANJA

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA INDEKS

VJEŽBE

SADRŽAJ INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

PODSJETNIK

SADRŽAJ NEODREĐENI INTEGRAL ODREĐENI INTEGRAL FUNKCIJE VIŠE VARIJABLA VIŠESTRUKI INTEGRALI DIFERENCIJALNE JEDNADŽBE METODA NAJMANJIH KVADRATA

JAVA NETPLOT OCTAVE Traži ...

☰   matematika2 Ekstremi funkcija više varijabla     FUNKCIJE VIŠE VARIJABLA     Uvjetni ekstremi

Implicitno zadane funkcije

U Matematici 1 smo već govorili o tome kako jednadžbu oblika

$$F(x,y)=0,$$

gdje je $F:\mathcal{D}\to \mathbb{R}$ , $\mathcal{D}\subseteq \mathbb{R}^2$ , neka funkcija dviju varijabla, možemo interpretirati i kao jednadžbu kojom je implicitno zadana neka funkcija jedne varijable

$$y=f(x),\qquad x\in I\subseteq \mathbb{R}.$$

Jednadžbi $F(x,y)=0$ prirodno pridružujemo skup $S\subseteq \mathbb{R}^2$ definiran s

$$S=\{(x,y)\in \mathcal{D}\mid F(x,y)=0\}$$

i u pravilu ga poistovjećujemo sa samom jednadžbom kojoj je pridružen.

Definicija 3.12   Za funkciju jedne varijable $f:I\to \mathbb{R}$ , gdje je $I\subseteq \mathbb{R}$ (obično je $I$ interval ili unija intervala u $\mathbb{R}$ ), za koju vrijedi

$$F(x,f(x))=0,\qquad \forall x\in I,$$

kažemo da je implicitno zadana jednadžbom $F(x,y)=0$ . Ovo iskazujemo i ekvivalentnim zahtjevom da je graf $\Gamma_f$ funkcije $f$ sadržan u skupu $S$ , odnosno

$$\Gamma_f =\{ (x,f(x))\mid x\in I\}\subseteq S.$$

Ova definicija zahtijeva dva komentara koja dajemo u sljedeće dvije napomene, zajedno s jednostavnim primjerima

Napomena 3.9   Ako je funkciju $f:I\to \mathbb{R}$ $I\subseteq \mathbb{R}$ implicitno zadana jednadžbom $F(x,y)=0$ , onda je prema definiciji 3.12 i svaka restrikcija $f:I'\to \mathbb{R}$ , $I'\subseteq I$ od $f$ implicitno zadana istom tom jednadžbom. Dakle, $F(x,y)=0$ u pravilu promatramo kao jednadžbu kojom je implicitno zadana ne jedna, već više funkcija jedne varijable, a dijelovi od $S$ grafovi su tih funkcija. Naravno, od interesa je slučaj kada postoji točno jedna osnovna funkcija $f$ koja je implicitno zadana tom jednadžbom i čiji se graf podudara s čitavim skupom $S$ , $\Gamma_f=S$ . Takvu funkciju $f$ nije uvijek moguće naći.

Primjer 3.18  

a)

Ako je funkcija $f$ zadana eksplicitno formulom

$$y=f(x),\quad x\in I \subseteq \mathbb{R},$$

onda je možemo shvatiti i kao funkciju koja je implicitno zadana jednadžbom

$$F(x,y)\equiv y-f(x)=0,$$

pri čemu je domena od $F$ skup $D=I\times\mathbb{R}$ , a skup $S$ je upravo graf $\Gamma_f$ zadane funkcije $f$ .

b)

Jednadžba

$$x^2+y^2-1=0$$

je implicitna jednadžbom kružnice sa središtem u ishodištu $(0,0)$ i polumjerom $1$ . Očito se radi o jednadžbi oblika $F(x,y)=0$ , gdje je $F(x,y)=x^2+y^2-1$ . U ovom slučaju funkcija $F(x,y)$ definirana je na $\mathcal{D}=\mathbb{R}^2$ , a pridruženi skup $S$ sastoji se od točaka $xy$ -ravnine koje su od ishodišta udaljene za $1$ . Kad tu jednadžbu razriješimo po varijabli $y$ kao nepoznanici dobivamo

$$y=\pm \sqrt{1-x^2},$$

odnosno $y$ nije jednoznačno određen. Zaključujemo da ne postoji jedna osnovna funkcija $f$ čiji se graf podudara sa $S$ . U stvari, jednadžbu $x^2+y^2-1=0$ obično interpretiramo kao jednadžbu kojom su implicitno zadane sljedeće dvije osnovne funkcije (vidi sliku 3.30)

$$f^{-}(x)=-\sqrt{1-x^2},\quad f^{+}(x)=\sqrt{1-x^2},\qquad x\in I=[-1,1].$$

Slika: Implicitno zadana kružnica

Međutim, i funkcija

$$f(x)=\left\{\begin{array}{rl}\sqrt{1-x^2},&\textrm{za } x\in [-1,0.5)\\ -\sqrt{1-x^2},&\textrm{za } x\in [0.5,1]\end{array}\right.$$

prikazana na slici 3.31) je također implicitno zadana jednadžbom $x^2+y^2-1=0$ .

Slika: Implicitno zadana funkcija izvedena iz kružnice

Napomena 3.10   Prema definiciji 3.12 jednadžbu $F(x,y)=0$ interpretiramo kao implicitnu vezu između varijabla $x$ i $y$ , pri čemu varijablu $x$ tretiramo kao nezavisnu, a varijablu $y$ kao zavisnu. Ponekad je pogodno zamijeniti uloge varijabla $x$ i $y$ .

Primjer 3.19  

a)

Jednadžbu

$$x+2=0$$

često interpretiramo kao jednadžbu pravca u ravnini koji prolazi točkom $(-2,0)$ na $x$ -osi i paralelan je s $y$ -osi. Jasno je da u toj jednadžbi varijablu $y$ ne možemo tretirati kao zavisnu jer se ona u njoj ne pojavljuje. Međutim, tu jednadžbu možemo interpretirati kao jednadžbu oblika $F(x,y)=0$ uz $F(x,y)=x+2$ , $(x,y)\in\mathbb{R}^2$ , u kojoj varijablu $y$ tretiramo kao nezavisnu. Stoga je tom jednadžbom implicitno zadana konstantna funkcija $x=f(y)=-2$ , $y\in I=\mathbb{R}$ .

b)

Jednadžbu

$$x+y^2=0$$

obično nazivamo implicitnom jednadžbom parabole. Tu je $F(x,y)=x+y^2$ definirana na $D=\mathbb{R}^2$ . Ako u toj jednadžbi varijablu $x$ interpretiramo kao nezavisnu, onda su njom implicitno zadane dvije osnovne funkcije čiji grafovi su dijelovi skupa $S$ pridruženog jednadžbi (vidi sliku 3.32). To su funkcije

$$y=f^{-}(x)=-\sqrt{-x},\quad y=f^{+}(x)=\sqrt{-x},\qquad x\in I=(-\infty,0].$$

Slika 3.32: Implicitno zadana parabola

S druge strane pogodnije je varijablu $y$ interpretirati kao nezavisnu jer se onda $x+y^2=0$ može interpretirati kao jednadžba kojom je implicitno zadana jedna osnovna funkcija

$$x=f(y)=-y^2,\qquad y\in I=\mathbb{R},$$

čiji graf se podudara sa skupom $S$ pridruženim toj jednadžbi.

Definiciju 3.12 na prirodan način poopćavamo na slučaj više varijabla.

Definicija 3.13   Neka je $F:X\to \mathbb{R}$ funkcija definirana na skupu $X\subseteq \mathbb{R}^{n+1}$ i neka je skup $S\subseteq \mathbb{R}^{n+1}$ definiran kao

$$S=\{(x_1,\cdots,x_n,x_{n+1})\in X\mid F(x_1,\cdots,x_n,x_{n+1})=0\}.$$

Za bilo koju funkciju $f:\mathcal{D}\to\mathbb{R}$ od $n$ varijabla koja je definirana na $\mathcal{D}\subseteq \mathbb{R}^n$ i za koju vrijedi

$$F(x_1,\cdots,x_n,f(x_1,\cdots,x_n))=0,\quad \forall (x_1,\cdots,x_n) \in \mathcal{D}$$

kažemo da je implicitno zadana jednadžbom

$$F(x_1,\cdots,x_n,x_{n+1})=0.$$

Ovo iskazujemo i ekvivalentnim zahtjevom da je graf $\Gamma_f$ funkcije $f$ sadržan u skupu $S$ :

$$\Gamma_f =\{(x_1,\cdots,x_n,f(x_1,\cdots,x_n))\mid (x_1,\cdots,x_n)\in \mathcal{D}\}\subseteq S.$$

Napomena 3.11   Primjedbe slične onima u napomeni 3.9 mogu se dati i uz definiciju 3.13. Jednadžbu

$$F(x_1,\cdots,x_n,x_{n+1})=0$$

uvijek promatramo kao jednadžbu kojom može biti implicitno zadano više funkcija od $n$ varijabla pri čemu varijablu $x_{n+1}$ tretiramo kao zavisnu, a varijable $x_1,\cdots,x_n$ kao nezavisne. Jasno je da i ovdje po potrebi možemo zamijeniti uloge varijabla, odnosno bilo koju varijablu možemo tretirati kao zavisnu, a preostale varijable kao nezavisne. U slučaju $n=2$ umjesto $x_1$ , $x_2$ i $x_3$ , često koristimo oznake $x$ , $y$ i $z$ .

Primjer 3.20  

a)

Jednadžbom

$$x^2+y^2-z^2=0$$

implicitno su zadana dva kružna stošca, oba s vrhom u ishodištu $(0,0,0)$ , jednom je os simetrije negativna $z$ -poluos, a drugomu pozitivna $z$ -poluos (vidi sliku 3.19).

Ovdje je funkcija $F(x,y,z)=x^2+y^2-z^2$ definirana na skupu $X=\mathbb{R}^3$ pa ako varijablu $z$ tretiramo kao zavisnu, onda su gornjom jednadžbom implicitno zadane dvije osnovne funkcije dviju nezavisnih varijabla $x$ i $y$ :

$$z=f^{-}(x,y)=-\sqrt{x^2+y^2},\quad z=f^{+}(x,y)=\sqrt{x^2+y^2}, \qquad (x,y)\in\mathbb{R}^2.$$

Ako bi u gornjoj jednadžbi varijablu $y$ tretirali kao zavisnu, onda su tom jednadžbom implicitno zadane dvije osnovne funkcije nezavisnih varijabla $x$ i $z$ :

$$y=f^{-}(x,z)=-\sqrt{z^2-x^2},\quad (x,z)\in D=\{(x,z)\in\mathbb{R}^2\mid \vert z\vert\leq \vert x\vert\}$$

i

$$y=f^{+}(x,z)=\sqrt{z^2-x^2},\quad (x,z)\in D=\{(x,z)\in\mathbb{R}^2\mid \vert z\vert\leq \vert x\vert\}.$$

Grafovi ovih funkcija su na slici 3.33.

Slika: Implicitno zadan stožac

b)

U jednadžbi

$$x+y^2+2y+z^2=0$$

je funkcija $F(x,y,z)=x+y^2+2y+z^2$ definirana na skupu $X=\mathbb{R}^3$ . Najjednostavnije je varijablu $x$ tretirati kao zavisnu jer je u tom slučaju ovom jednadžbom implicitno zadana točno jedna osnovna funkcija dviju nezavisnih varijabla $y$ i $z$ ,

$$x=f(y,z)=-y^2-2y-z^2,\qquad (y,z)\in\mathbb{R}^2.$$

Ova jednadžba se može ekvivalentno zapisati kao

$$x-1=-(y+1)^2-z^2,$$

što je jednadžba kružnog paraboloida s vrhom u točki $(1,-1,0)$ okrenutog u smjeru negativne $x$ -poluosi. Paraboloid je sličan onome na slici 3.16 uz pomaknuti vrh.

Zanima nas koji su dovoljni uvjeti da bi formulom $F(x_1,\cdots,x_m,x_{m+1})=0$ bila implicitno zadana funkcija $f$ takva da je

$$x_{n+1}=f(x_1,\cdots,x_n)$$

i koja su svojstva tako zadane funkcije? Odgovore daje sljedeći teorem.

Teorem 3.9   Neka je $F:X\to \mathbb{R}$ funkcija definirana na otvorenom skupu $X\subseteq \mathbb{R}^{n+1}$ koja ima neprekidne sve parcijalne derivacije u svim točkama skupa $X$ (dakle, $F$ je diferencijabilna u svim točkama skupa $X$ ). Neka za točku $T_0=(x_1^0,\cdots,x_n^0,x_{n+1}^0)\in X$ vrijedi

$$F(x_1^0,\cdots,x_n^0,x_{n+1}^0)=0,\quad F'_{x_{n+1}} (x_1^0,\cdots,x_n^0,x_{n+1}^0)\neq 0.$$

Tada vrijedi sljedeće:

i.

Postoji okolina $\mathcal{D}\subseteq \mathbb{R}^n$ točke $(x_1^0,\cdots,x_n^0)$ i samo jedna funkcija $f:\mathcal{D}\to\mathbb{R}$ za koju je

$$x_{n+1}^0=f(x_1^0,\cdots,x_n^0)$$

i vrijedi

$$F(x_1,\cdots,x_n,f(x_1,\cdots,x_n))=0,\quad \forall (x_1,\cdots,x_n)\in \mathcal{D}.$$

ii.

Funkcija $f$ ima neprekidne parcijalne derivacije $f'_{x_i}$ na $\mathcal{D}$ po svim varijablama $x_i$ , $i=1,\cdots,n$ . U svakoj točki $(x_1,\cdots,x_n)\in \mathcal{D}$ vrijedi

$$f'_{x_i}(x_1,\cdots,x_n)=-\frac{F'_{x_i}(x_1,\cdots,x_n,x_{n+1})} {F'_{x_{n+1}}(x_1,\cdots,x_n,x_{n+1})},\qquad i=1,\cdots,n,$$

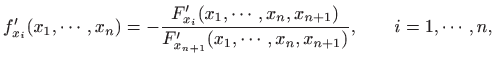
pri čemu je

$$x_{n+1}=f(x_1,\cdots,x_n).$$

Napomena 3.12  

a)

Kada imamo implicitnu vezu dviju varijabla

$$F(x,y)=0$$

definiranu pomoću funkcije $F:X\to \mathbb{R}$ koja na $X\subseteq \mathbb{R}^2$ ima neprekidne parcijalne derivacije $F'_x$ i $F'_y$ , teorem 3.9 kaže da će za svaku točku $(x_0,y_0)\in X$ u kojoj vrijedi

$$F(x_0,y_0)=0,\qquad F'_y(x_0,y_0)\neq 0$$

postojati okolina $\mathcal{D}\subseteq \mathbb{R}$ od $x_0$ i samo jedna funkcija $f:\mathcal{D}\to\mathbb{R}$ koja je implicitno zadana s $F(x,y)=0$ i koja je neprekidno derivabilna na $D$ . Derivacija $f'(x)$ u točki $x\in D$ je

$$f'(x)=-\frac{F'_x(x,y)}{F'_y(x,y)},\qquad F(x,y)=0.$$

b)

U slučaju implicitne veze triju varijabla

$$F(x,y,z)=0$$

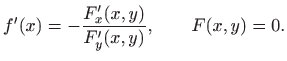
definirane pomoću funkcije $F:X\to \mathbb{R}$ koja na $X\subseteq \mathbb{R}^3$ ima neprekidne parcijalne derivacije $F'_x$ , $F'_y$ i $F'_z$ , teorem 3.9 kaže da će za svaku točku $(x_0,y_0,z_0)\in X$ u kojoj je

$$F(x_0,y_0,z_0)=0,\qquad F'_z(x_0,y_0,z_0)\neq 0$$

postojati okolina $\mathcal{D}\subseteq \mathbb{R}^2$ točke $(x_0,y_0)$ i samo jedna funkcija $f:\mathcal{D}\to\mathbb{R}$ koja je implicitno zadana s $F(x,y,z)=0$ i koja ima neprekidne parcijalne derivacije $f'_x$ i $f'_y$ na $\mathcal{D}$ . Parcijalne derivacije $f'_x(x,y)$ i $f'_y(x,y)$ u točki $(x,y)\in \mathcal{D}$ su

$$f'_x(x,y) =-\frac{F'_x(x,y,z)}{F'_z(x,y,z)},$$

$$f'_y(x,y) =-\frac{F'_y(x,y,z)}{F'_z(x,y,z)},$$

$$F(x,y,z) =0.$$

Primjer 3.21  

a)

U primjeru 3.19 b) vidjeli smo da su jednadžbom

$$x+y^2=0$$

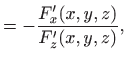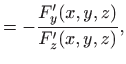implicitno zadane dvije osnovne funkcije nezavisne varijable $x$

$$y=f^{-}(x)=-\sqrt{-x},\quad y=f^{+}(x)=\sqrt{-x},\qquad x\in I=(-\infty,0].$$

Ovdje je $F(x,y)=x+y^2$ definirana i neprekidno derivabilna na $X=\mathbb{R}^2$ te su joj parcijalne derivacije dane formulama

$$F'_x(x,y)=1,\qquad F'_y(x,y)=2y.$$

U točki $(-4,-2)$ imamo

$$F(-4,-2)=0,\qquad F'_x(-4,-2)=1,\qquad F'_y(-4,-2)=-4.$$

Pretpostavke teorema 3.9 ispunjene su i zato mora postojati okolina $\mathcal{D}\subseteq \mathbb{R}$ od $-4$ i samo jedna derivabilna funkcija $f:\mathcal{D}\to\mathbb{R}$ implicitno zadana jednadžbom $x+y^2=0$ . Očito je to funkcija $f^{-}$ . Međutim, tu funkciju ne možemo gledati na čitavom skupu $I=(-\infty,0]$ , već samo na podskupu $D=(-\infty,0)$ , jer u točki 0 nije derivabilna. Dakle,

$$f(x)=-\sqrt{-x},\qquad x\in D=(-\infty,0),$$

Da bi izračunali na primjer $f'(-4)$ ne treba nam eksplicitni izraz za $f'(x)$ , već imamo

$$f'(-4)=-\frac{F'_x(-4,-2)}{F'_y(-4,-2)}=-\frac{1}{-4}=\frac{1}{4}.$$

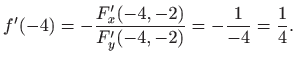
U ovom slučaju gornji račun možemo provjeriti koristeći eksplicitni izraz

$$f'(x)=\frac{1}{2 \sqrt{-x}},\qquad x\in \mathcal{D}=(-\infty,0).$$

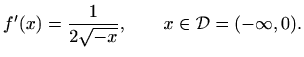
Jasno je da, općenito, takvu provjeru nećemo moći napraviti jer funkciju $f$ nećemo imati eksplicitno zadanu, već ćemo samo znati da postoji. Uočimo još da i točka $(0,0)$ zadovoljava $F(0,0)=0$ , ali teorem 3.9 u toj točki nije primjenjiv jer je $F'_y(0,0)=0$ .

b)

Promotrimo jednadžbu

$$xyz-e^{-xyz}=0$$

kao implicitnu vezu triju varijabla. Zbog očite simetrije svejedno je koju varijablu tretiramo kao zavisnu pa uzmimo da je to varijabla $z$ . Imamo

$$F(x,y,z)=xyz-e^{-xyz},\qquad (x,y,z)\in X=\mathbb{R}^3$$

i u svim točkama $(x,y,z)\in X$ vrijedi

$$F'_x(x,y,z) =\left(1+e^{-xyz}\right)yz,$$

$$F'_y(x,y,z) =\left(1+e^{-xyz}\right)xz,$$

$$F'_z(x,y,z) =\left(1+e^{-xyz}\right)xy.$$

Kako je

$$1+e^{-xyz}>1,\qquad \forall (x,y,z)\in X,$$

imamo

$$F'_z(x,y,z)=\left(1+e^{-xyz}\right)xy=0 \quad \Leftrightarrow \quad x=0 \vee y=0.$$

Prema tome, teorem 3.9 možemo primijeniti u svakoj točki $(x,y,z)\in X$ u kojoj je zadovoljena početna jednadžba i za koju je $x\neq 0$ i $y\neq 0$ . Dakle, za svaku takvu točku postojat će okolina $\mathcal{D}\subseteq \mathbb{R}^2$ i samo jedna funkcija $f$ nezavisnih varijabla $x$ i $y$ koja je implicitno zadana početnom jednadžbom i neprekidno derivabilna na $\mathcal{D}$ . Za parcijalne derivacije funkcije $f$ vrijedit će

$$f'_x(x,y) =-\frac{F'_x(x,y,z)}{F'_z(x,y,z)}=-\frac{z}{x},$$

$$f'_y(x,y) =-\frac{F'_x(x,y,z)}{F'_z(x,y,z)}=-\frac{z}{y}.$$

Naravno, za konkretno zadane vrijednosti $x\neq 0$ i $y\neq 0$ pripadajuća vrijednost varijable $z$ je jednoznačno određena početnom jednadžbom i ne možemo je egzaktno izraziti pomoću elementarnih funkcija varijabla $x$ i $y$ . Međutim, i u ovom primjeru možemo gornje formule za parcijalne derivacije provjeriti neposrednim deriviranjem slično kao u prethodnom primjeru. Naime, uvođenjem pomoćne varijable $t=xyz$ početnu jednadžbu možemo napisati kao

$$t=e^{-t},\qquad t=xyz.$$

Krivulja $y=e^{-x}$ i pravac $y=x$ sijeku se točno u jednoj točki s apscisom $c\in (0,1)$ kako se vidi na slici 3.34.

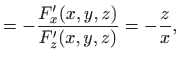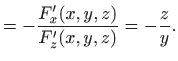Slika: Sjecište krivulja

Stoga jednadžba $t=e^{-t}$ ima točno jedno rješenje $t=c$ . Veličinu $c$ ne možemo egzaktno izraziti koristeći elementarne funkcije jedne varijable, već samo možemo upotrijebiti neku od elementarnih numeričkih metoda (na primjer metodu bisekcije - za računanje možete koristiti i ogovarajući java aplet) da bi dobili približnu vrijednost od $c$ (vrijedi $c\approx 0.56$ ). Zaključujemo da je početna jednadžba ekvivalentna s jednadžbom

$$xyz=c$$

iz koje dobivamo eksplicitno varijablu $z$ kao funkciju varijabla $x$ i $y$ (vidi sliku 3.35),

$$z=f(x,y)=\frac{c}{xy},\qquad x\neq 0 \wedge y\neq 0.$$

Sada neposrednim deriviranjem dobijamo

$$f'_x(x,y)=-\frac{c}{x^2y}=-\frac{z}{x},\qquad f'_y(x,y)=-\frac{c}{xy^2}=-\frac{z}{y}.$$

Slika 3.35: Implicitno zadana funkcija

Ekstremi funkcija više varijabla     FUNKCIJE VIŠE VARIJABLA     Uvjetni ekstremi