Neka je područje
![]() zadano u polarnom koordinatnom
sustavu kao
zadano u polarnom koordinatnom
sustavu kao
gdje su
Formula za površinu kružnog isječka daje
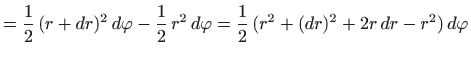 |
||
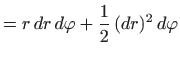 |
||
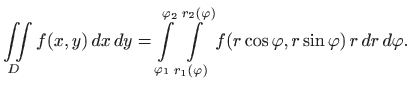
Uočimo da se u polarnim koordinatama uvijek integrira prvo po ![]() pa onda po
pa onda po ![]() .
Opće pravilo zamjene varijabli u višestrukom integralu dano je u poglavlju
4.4.
.
Opće pravilo zamjene varijabli u višestrukom integralu dano je u poglavlju
4.4.
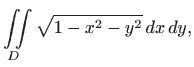
gdje je
Da bi područje ![]() opisali u polarnim koordinatama, potrebno je naći odgovarajuću
jednadžbu zadane kružnice. Uvrštavanje supstitucije (4.2) u
jednadžbu kružnice daje
opisali u polarnim koordinatama, potrebno je naći odgovarajuću
jednadžbu zadane kružnice. Uvrštavanje supstitucije (4.2) u
jednadžbu kružnice daje
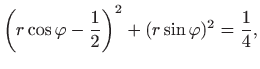
odnosno
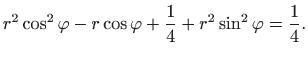
Vrijedi
Dakle, područje
pa je
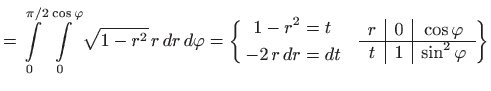 |
||
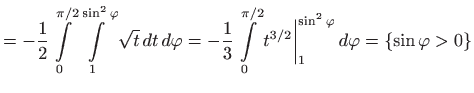 |
||
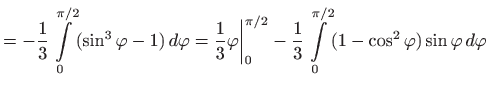 |
||
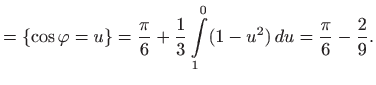 |