Dvostruki integral koristimo za računanje volumena (obujma) i površine. Neka je
podintegralna funkcija
![]() ,
,
![]() , neprekidna (tada je i
omeđena) i nenegativna, i neka je područje
, neprekidna (tada je i
omeđena) i nenegativna, i neka je područje ![]() omeđeno po dijelovima glatkom
jednostavnom zatvorenom krivuljom4.2.
Tada je vrijednost pripadnog dvostrukog integrala
jednaka volumenu tijela
omeđeno po dijelovima glatkom
jednostavnom zatvorenom krivuljom4.2.
Tada je vrijednost pripadnog dvostrukog integrala
jednaka volumenu tijela ![]() koje je omeđeno bazom
koje je omeđeno bazom ![]() u
u
![]() -ravnini i plohom
-ravnini i plohom ![]() ,
,
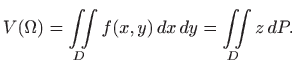
Izraz
Ako je
![]() , onda dvostruki integral daje površinu područja
, onda dvostruki integral daje površinu područja ![]() (volumen tijela s bazom
(volumen tijela s bazom ![]() visine 1 jednak je površini baze):
visine 1 jednak je površini baze):
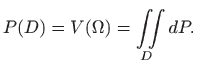
i plohom
Rastavljajući područje integracije na dva dijela imamo
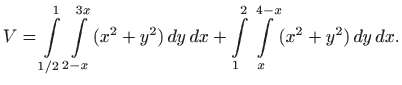
Alternativno, rastavljajući područje integracije na tri dijela i integrirajući prvo po varijabli
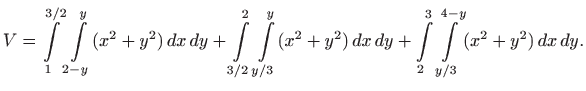
Riješite primjer do kraja na oba načina.
Nadalje, neka je tijelo ![]() omeđeno plohama
omeđeno plohama ![]() i
i ![]() , pri
čemu je
, pri
čemu je
a