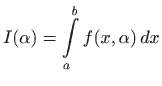
U ovom poglavlju opisat ćemo postupke deriviranja i integriranja integrala ovisnih o parametru, kao i primjene tih postupaka na rješavanje nekih određenih integrala. Također ćemo obraditi gama i beta funkcije.
Promotrimo integral
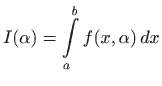
u kojem integrand
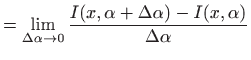 |
||
![$\displaystyle =\lim_{\Delta \alpha \to 0} \frac{1}{\Delta \alpha} \left[ \in...
...ts _a^b f(x,\alpha+\Delta \alpha) dx-\int\limits _a^b f(x,\alpha) dx\right]$](img2313.gif) |
||
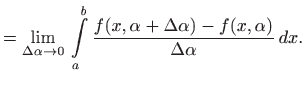 |
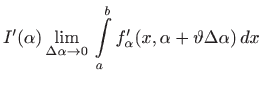
za neki
U slučaju kada i granice integracije ovise o parametru, vrijedi:
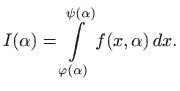
Tada za svaki
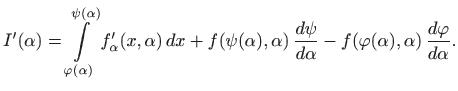
pravilo za deriviranje kompozicije funkcija (teorem 3.5) daje
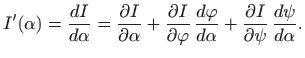
Prema teoremu 4.3 je
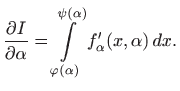
Neka je
![$\displaystyle =\frac{\partial}{\partial \psi} \int\limits _{\varphi(\alpha)}^{\...
...ial \psi} \left[ F(x,\alpha)\bigg\vert _{\varphi(\alpha)}^{\psi(\alpha)}\right]$](img2329.gif) |
||
![$\displaystyle =\frac{\partial}{\partial \psi} \left[ F(\psi(\alpha),\alpha)- F(\varphi(\alpha),\alpha)\right] = f(\psi(\alpha),\alpha).$](img2330.gif) |
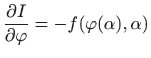
pa tvrdnja teorema slijedi iz četiri prethodne relacije.
Prethodne teoreme koristimo za rješavanje nekih diferencijalnih jednadžbi, računanje Fourierovih koeficijenata i nalaženje nekih određenih integrala.
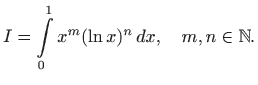
Vrijedi
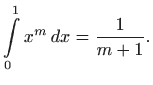
Funkcije
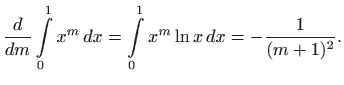
Nakon još jednog deriviranja imamo
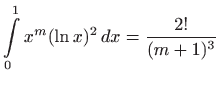
iz čega zaključujemo da
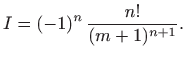
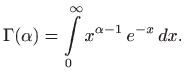
Za
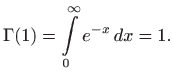
Za
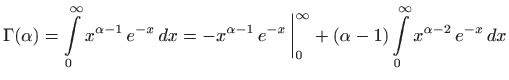
iz čega slijedi
Stoga za
Beta funkcija ili Eulerov integral prve vrste je integral
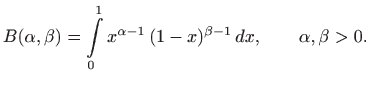
Beta funkcija je simetrična s obzirom na svoje parametre, odnosno vrijedi
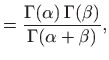 |
||
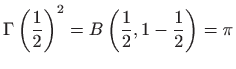
pa je
Gama funkcija i beta funkcija javljaju se u brojnim aplikacijama i po važnosti su odmah iza elementarnih funkcija.