Ako ![]() i
i ![]() imaju zajedničku nul-točku
imaju zajedničku nul-točku ![]() , odnosno ako je
, odnosno ako je
onda je
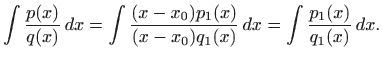
Zadnja jednakost vrijedi jer se prema definiciji 1.1 integral ne mijenja ako se podintegralna funkcija promijeni u prebrojivo mnogo točaka.
Postupak možemo nastaviti sve dok ne dobijemo racionalnu funkciju u
kojoj brojnik i nazivnik nemaju zajedničkih nul-točaka.
U nastavku izlaganja stoga pretpostavljamo da ![]() i
i ![]() nemaju
zajedničkih nul-točaka.
nemaju
zajedničkih nul-točaka.