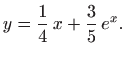| (5.14) |
Sljedeći teorem daje opće rješenje linearne diferencijalne jednadžbe drugog reda
Prema teoremu 5.3 rješenje homogene jednadžbe je oblika
Uvrštavanjem dobivamo sustav linearnih jednadžbi u nepoznanicama
Partikularno rješenje nalazimo
metodom varijacije konstanti. Neka
je
![]() rješenje pripadne homogene jednadžbe pri čemu su
rješenje pripadne homogene jednadžbe pri čemu su
![]() i
i ![]() linearno nezavisne funkcije. Partikularno rješenje nehomogene
jednadžbe tražimo u istom obliku, s tom razlikom što pretpostavljamo da
linearno nezavisne funkcije. Partikularno rješenje nehomogene
jednadžbe tražimo u istom obliku, s tom razlikom što pretpostavljamo da ![]() i
i ![]() nisu konstante, već neke funkcije od
nisu konstante, već neke funkcije od ![]() . Deriviranje daje
. Deriviranje daje
Odaberimo funkcije
pa je
Uvrštavanje u jednadžbu (5.14) daje
odnosno
Kako su
Kombinirajući ovu jednakost s jednakošću (5.15), vidimo da su funkcije
onda je, konačno,
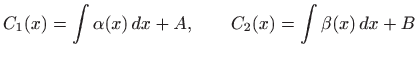
pri čemu su
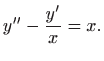
Prvo nađimo opće rješenje homogene jednadžbe
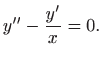
Iz
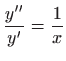
slijedi
pa je
Partikularno rješenje ćemo odrediti metodom varijacije konstanti: funkcije
Dakle,
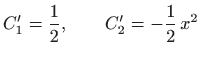
pa je
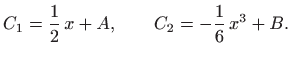
Stoga je, uz
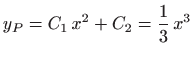
pa je opće rješenje jednako
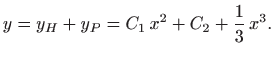
jednako
Na primjer, partikularno rješenje jednadžbe
jednako