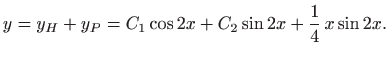| (5.17) |
Linearna diferencijalna jednadžba drugog reda s konstantnim koeficijentima glasi
odnosno
Kako je eksponencijalna funkcija uvijek nenegativna,
Dakle, vrijedi
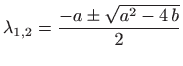
pa razlikujemo tri slučaja.
Ako je
![]() , nul-točke su različite i realne,
, nul-točke su različite i realne,
![]() ,
,
![]() .
Onda su
.
Onda su
dva linearno nezavisna rješenja homogene jednadžbe jer je
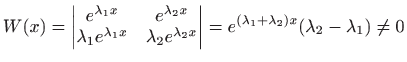
pa je
Ako je
![]() , onda imamo jednu dvostruku realnu nul-točku,
, onda imamo jednu dvostruku realnu nul-točku,
Dva linearno nezavisna rješenja homogene jednadžbe jednaka su
pa je
Zaista, funkcija
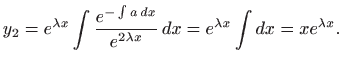
Ako je
![]() , nul-točke su konjugirano kompleksne,
, nul-točke su konjugirano kompleksne,
![]() , odnosno
, odnosno
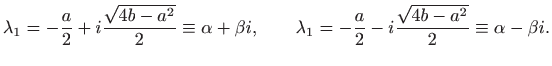
Onda su
dva linearno nezavisna rješenja homogene jednadžbe kao i u prvom slučaju. No, prema teoremu 5.2, i funkcije
![$\displaystyle =\displaystyle \frac{y_1+y_2}{2}=\frac{1}{2} [e^{(\alpha+\beta i) x}+e^{(\alpha-\beta i) x}]$](img3165.gif) |
||
![$\displaystyle = \frac{1}{2} [e^{\alpha x}(\cos \beta x+i\sin\beta x) + e^{\alpha x}(\cos \beta x-i\sin\beta x)]$](img3166.gif) |
||
![$\displaystyle y_4=\displaystyle \frac{y_1-y_2}{2i}=\frac{1}{2i} [e^{(\alpha+\beta i)
x}-e^{(\alpha-\beta i) x}]=e^{\alpha x}\sin \beta x
$](img3168.gif)
također su rješenja jednadžbe (5.18). Pomoću Wronskijana vidimo da su funkcije
karakteristična jednadžba glasi
Stoga je
glasi
Stoga je
Karakteristična jednadžba glasi
Rješenja su konjugirano kompleksna,
pa je
Prvi uvjet daje
Kako je
drugi uvjet daje
odnosno
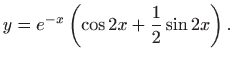
Nakon što smo izračunali rješenje homogene jednadžbe (5.18),
partikularno rješenje ![]() jednadžbe (5.17) možemo naći ili metodom varijacije
konstanti iz poglavlja 5.9.2
ili metodom neodređenih koeficijenata
koja je opisana na kraju ovog poglavlja.
jednadžbe (5.17) možemo naći ili metodom varijacije
konstanti iz poglavlja 5.9.2
ili metodom neodređenih koeficijenata
koja je opisana na kraju ovog poglavlja.
Karakteristična jednadžba glasi
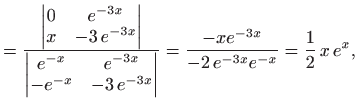 |
||
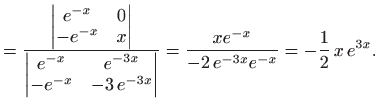 |
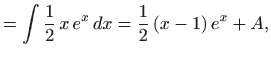 |
||
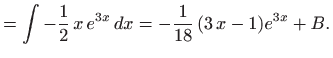 |
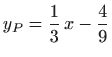
pa je opće rješenje zadane jednadžbe jednako
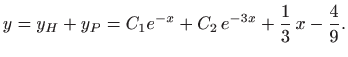
Ukoliko funkcija ![]() u jednadžbi (5.17) ima poseban oblik,
u jednadžbi (5.17) ima poseban oblik,
Uvrštavanje u zadanu jednadžbu daje
Izjednačavanje lijeve i desne strane po potencijama od
pa je partikularno rješenje jednako
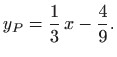
Ovaj postupak je jednostavniji od metode varijacije konstanti koju smo koristili u primjeru 5.24.
Rješenje homogene jednadžbe je
Funkcija
Uvrštavanje
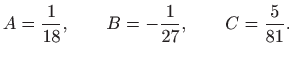
Dakle, partikularno rješenje je jednako
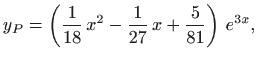
a opće rješenje zadane jednadžbe je
Nul-točke karakteristične jednadžbe su
Funkcija
Uvrštavanje
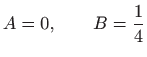
pa je opće rješenje zadane jednadžbe jednako