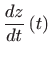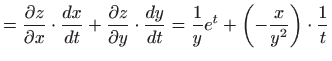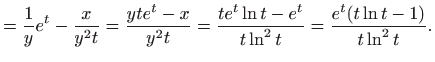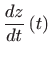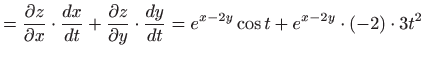☰
matematika2
Totalni diferencijal drugog reda
FUNKCIJE VIŠE VARIJABLA
Parcijalne derivacije složene funkcije
Derivacija složene funkcije jedne varijable
Odredite derivaciju
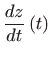 ako je:
ako je:
- a)
-
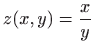 ,
,
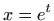 ,
,
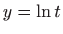 ,
,
- b)
-
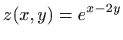 ,
,
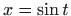 ,
,
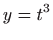 .
.
Rješenje.
Primijenjujemo
![[*]](../icons.gif/crossref.gif) [M2, teorem 3.5]:
[M2, teorem 3.5]:
- a)
-
- b)
-
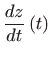 ako je:
ako je:
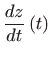 ako je:
ako je:
![]() [M2, teorem 3.5]:
[M2, teorem 3.5]: