Zanimljiv i koristan zadatak, čije rješenje se svodi na diferencijalnu jednadžbu drugog reda
s konstantnim koeficijentima, je odrediti ponašanje sustava koji se sastoji od
mase, opruge i prigušenja (amortizera). Tijelo mase ![]() titra
na opruzi koja ima koeficijent opruge
titra
na opruzi koja ima koeficijent opruge ![]() . Sustav ima dodatno trenje (gušenje)
s koeficijentom gušenja
. Sustav ima dodatno trenje (gušenje)
s koeficijentom gušenja ![]() , a na tijelo djeluje vanjska sila
, a na tijelo djeluje vanjska sila ![]() .
.
Neka je ![]() otklon tijela od položaja mirovanja u trenutku
otklon tijela od položaja mirovanja u trenutku ![]() . Na tijelo
djeluju sljedeće sile:
. Na tijelo
djeluju sljedeće sile:
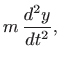
U najjednostavnijem slučaju kada nema ni gušenja ni vanjske sile (![]() i
i
![]() ), radi se o harmonijskom oscilatoru. Pripadna (homogena) diferencijalna jednadžba glasi
), radi se o harmonijskom oscilatoru. Pripadna (homogena) diferencijalna jednadžba glasi
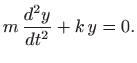
Karakteristična jednadžba je
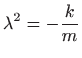
pa jednažba titranja glasi
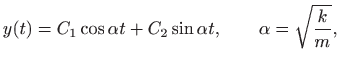
što je periodička funkcija s periodom
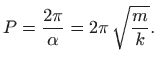
Konstante
pa adicijski teorem (vidi
U slučaju kada nema vanjske sile, diferencijalna jednadžba je homogena i glasi
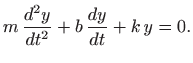
Karakteristična jednadžba glasi
pa je
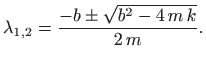
U skladu s razmatranjima iz poglavlja 5.9.3 razlikujemo tri slučaja:
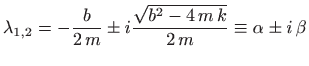
pa je rješenje diferencijalne jednadžbe jednako
U sva tri slučaja vrijedi
![]() . U prvom slučaju radi se
o gušenju bez titranja, u drugom slučaju može doći do jednokratnog porasta početnog otklona
nakon čega nastupa gušenje bez titranja, a u trećem slučaju radi se o gušenom titranju oko
položaja ravnoteže. Primjeri ponašanja sustava dani su na slici 5.17.
. U prvom slučaju radi se
o gušenju bez titranja, u drugom slučaju može doći do jednokratnog porasta početnog otklona
nakon čega nastupa gušenje bez titranja, a u trećem slučaju radi se o gušenom titranju oko
položaja ravnoteže. Primjeri ponašanja sustava dani su na slici 5.17.
Ukoliko na sustav djeluje i vanjska sila ![]() , radi se o
prisilnim oscilacijama.
Sustav je opisan nehomogenom jednadžbom (5.22).
Analizirat ćemo ponašanje sustava kada je
vanjska sila jednaka
, radi se o
prisilnim oscilacijama.
Sustav je opisan nehomogenom jednadžbom (5.22).
Analizirat ćemo ponašanje sustava kada je
vanjska sila jednaka
Kao što smo već vidjeli, kod rješavanja pripadne homogene jednadžbe razlikujemo tri slučaja. U prvom slučaju, kada je
Partikularno rješenje možemo naći metodom neodređenih koeficijenta koja je opisana u poglavlju 5.9.3. Iz formula (5.20) i (5.21) zaključujemo da partikularno rješenje ima oblik
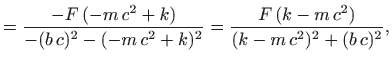 |
||
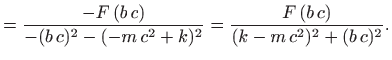 |
možemo pisati
![$\displaystyle y_P=\frac{F}{[h(c)]^2} [ (k-m c^2)\cos ct + (b c) \sin ct],
$](img3310.gif)
a uz oznake
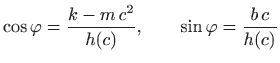
slijedi uobičajeni oblik partikularnog rješenja
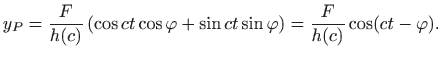
Dosadašnje razmatranje omogućava nam uvid u ponašanje zadanog sustava. Opće rješenje jednadžbe (5.22),
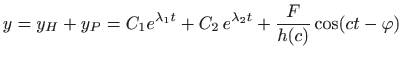
sastoji se od dva dijela. Prvi dio,
Promotrimo još sustav s prisilnim oscilacijama bez gušenja (![]() ) čija
jednadžba glasi
) čija
jednadžba glasi
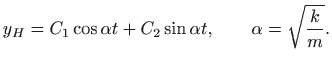
Razlikujemo dva slučaja. Ako je
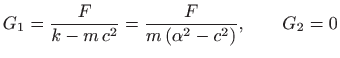
pa je opće rješenje jednadžbe (5.26) jednako
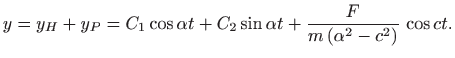
Uz oznake (5.23) imamo
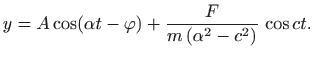
Vidimo da je opće rješenje jednadžbe (5.26) zbroj dvaju periodičkih funkcija s periodima
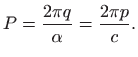
U protivnom
Potencijalno najopasniji je slučaj kada je ![]() , odnosno kada vanjska sila
i rješenje homogene jednadžbe imaju istu frekvenciju. Tada nastaje fenomen mehaničke
rezonancije sustava.
Prema formulama (5.20) i
(5.21) partikularno rješenje ima oblik
, odnosno kada vanjska sila
i rješenje homogene jednadžbe imaju istu frekvenciju. Tada nastaje fenomen mehaničke
rezonancije sustava.
Prema formulama (5.20) i
(5.21) partikularno rješenje ima oblik
Uvrštavanje
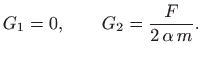
Dakle, opće rješenje jednadžbe (5.26) u ovom slučaju glasi
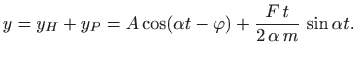
Ovo je periodička funkcija s periodom
Na kraju, primijetimo da mehanički sustav koji se sastoji od mase, opruge i gušača ima
svoj električni ekvivalent.
Promotrimo strujni krug koji se sastoji od kondenzatora kapaciteta ![]() farada
(F), otpora od
farada
(F), otpora od ![]() oma (Ohm) i zavojnice s induktivitetom
oma (Ohm) i zavojnice s induktivitetom ![]() henrija (H), a
na koji djeluje elektromotorna sila
koja u trenutku
henrija (H), a
na koji djeluje elektromotorna sila
koja u trenutku ![]() proizvodi napon od
proizvodi napon od ![]() volta (V) i struju od
volta (V) i struju od ![]() ampera (A) (usporedi s primjerom 5.2). Krug je prikazan na slici
5.20.
ampera (A) (usporedi s primjerom 5.2). Krug je prikazan na slici
5.20.
Prema Ohmovom zakonu pad napona na otporu jednak je
![]() . Pad napona na zavojnici jednak je
. Pad napona na zavojnici jednak je ![]() , a pad napona na
kondenzatoru jednak je
, a pad napona na
kondenzatoru jednak je ![]() , pri čemu je
, pri čemu je ![]() naboj pozitivne ploče
kondenzatora. Prema Kirchoffovom zakonu zbroj padova
napona jednak je naponu kojeg daje naponski izvor, odnosno
naboj pozitivne ploče
kondenzatora. Prema Kirchoffovom zakonu zbroj padova
napona jednak je naponu kojeg daje naponski izvor, odnosno
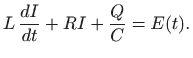
Iz ove jednadžbe možemo dobiti linearnu jednadžbu drugog reda na dva načina: uvrštavanje
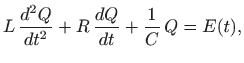
dok deriviranje daje
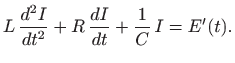
Uspoređujući obje prethodne jednadžbe s jednadžbom (5.22) zaključujemo da je zavojnica ekvivalentna s masom, otpor s gušačem, a kondenzator s oprugom. Također zaključujemo da prijelazna faza rješenje odgovara zagrijavanju električnog uređaja (na primjer, televizije), dok je otpor nužan radi izbjegavanja rezonancije sustava.