U ovom poglavlju opisat ćemo postupke rješavanja sustava linearnih diferencijalnih jednadžbi oblika
Zanimljiv primjer je sustav grabežljivac-plijen (engleski predator-prey).
Zamislimo sustav u kojem postoji populacija
grabežljivaca (lovaca) i plijena (žrtve). Neka su, na primjer, grabežljivci vukovi, a plijen
zečevi. Označimo redom populacije vukova i zečeva s ![]() i
i ![]() .
Izvedimo model ponašanja obaju populacija.
Ukoliko nema vukova, pretpostavljamo da se zečevi razmnožavaju u skladu s populacijskom
jednadžbom iz poglavlja 5.1,
.
Izvedimo model ponašanja obaju populacija.
Ukoliko nema vukova, pretpostavljamo da se zečevi razmnožavaju u skladu s populacijskom
jednadžbom iz poglavlja 5.1,
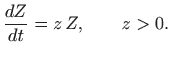
Ukoliko nema zečeva, populacija vukova će odumirati, opet u skladu s populacijskom jednadžbom,
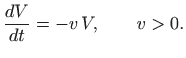
Ukoliko u sustavu postoje obje populacije, onda će zbog međusobnih susreta populacija zečeva nazadovati, dok će populacija vukova napredovati. Ukoliko vjerojatnost susreta modeliramo produktom
Ako je, na primjer,
sustav jednadžbi glasi
Sustav (5.32) nije moguće direktno riješiti. No, oblik sustava
omogućava primjenu Eulerove metode iz poglavlja
5.4 pomoću koje možemo naći približno
numeričko rješenje.
Sljedeći Matlab program računa i crta ponašanje sustava
(5.32) uz početne uvjete ![]() i
i ![]() . Rješenja su prikazana
na slici 5.21.5.9
. Rješenja su prikazana
na slici 5.21.5.9
Octave On-line[Octave On-line Home] [Octave User's Guide] |
Sustav jednadžbi (5.32) može se egzaktno riješiti u faznom
prostoru varijabla ![]() i
i ![]() (jednu od tih varijabla
tretiramo kao funkciju druge). Vrijedi
(jednu od tih varijabla
tretiramo kao funkciju druge). Vrijedi
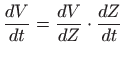
iz čega slijedi jednadžba koja povezuje populacije vukova i zečeva:
Jednadžba (5.33) je jednadžba sa separiranim varijablama (vidi poglavlje 5.2) za koju je lako izračunati egzaktno rješenje. Vrijedi:
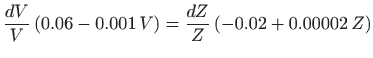
pa je
Dakle,
odnosno rješenje jednadžbe dano je implicitno zadanom funkcijom
Ako su zadani početni uvjeti
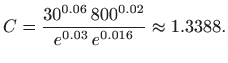
Funkcija je prikazana na slici 5.23.
Na kraju poglavlja opisat ćemo postupak rješavanja jednostavnih sustava diferencijalnih jednadžbi oblika
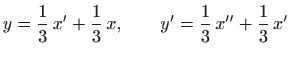
pa uvrštavanje u drugu jednadžbu daje
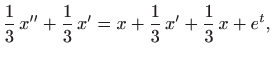
odnosno
Uvrštavanjem partikularnog rješenja oblika
Deriviranje daje
pa je
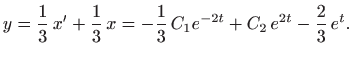
Dakle, opće rješenje zadanog sustava (bez zadanih uvjeta) glasi
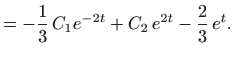 |
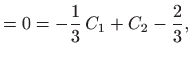 |
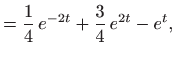 |
||
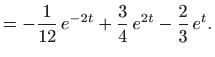 |
Linearna diferencijalna jednadžba reda ![]() može se svesti na sustav od
može se svesti na sustav od
![]() linearnih diferencijalnih jednadžbi prvog reda.
linearnih diferencijalnih jednadžbi prvog reda.
Supstitucije
daju sustav