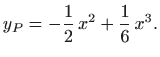| (5.27) |
U ovom poglavlju poopćit ćemo rezultate iz poglavlja 5.9 na linearne jednadžbe višeg reda. Dokazi tvrdnji su slični dokazima iz poglavlja 5.9 pa ih izostavljamo.
Linearna diferencijalna jednadžba višeg reda glasi
Pripadna homogena jednadžba glasi
Za ![]() funkcija
funkcija
![]() kažemo da su linearno
nezavisne na intervalu
kažemo da su linearno
nezavisne na intervalu
![]() ako relacija
ako relacija
povlači
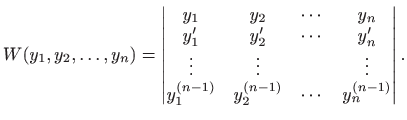
Wronskijan ili nikad nije nula ili je identično jednak nuli na intervalu
Opće rješenje jednadžbe (5.27) ima oblik
gdje je
pri čemu linearno nezavisne funkcije
Ukoliko znamo rješenje nehomogene jednadžbe, partikularno rješenje
nehomogene jednadžbe možemo naći metodom varijacije
konstanti.
Partikularno rješenje, ![]() , ima isti oblik kao i rješenje homogene jednadžbe
, ima isti oblik kao i rješenje homogene jednadžbe
![]() , s tom razlikom što pretpostavljamo da
, s tom razlikom što pretpostavljamo da ![]() nisu konstante već funkcije od
nisu konstante već funkcije od ![]() . Formiramo sustav od
. Formiramo sustav od ![]() linearnih
jednadžbi u varijablama
linearnih
jednadžbi u varijablama ![]() :
:
Linearna diferencijalna jednadžba višeg reda s konstantnim koeficijentima glasi
pa su vrijednosti
Linearno nezavisna rješenja homogene jednadžbe formiramo ovisno o karakteru rješenja karakteristične jednadžbe prema sljedećim pravilima:
karakteristična jednadžba glasi
Rješenja karakteristične jednadžbe su
Sustav (5.29) glasi
Integriranje daje
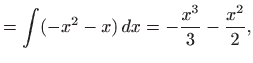 |
||
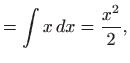 |
||
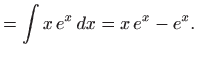 |
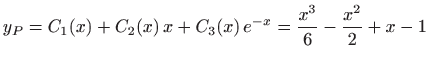
pa je opće rješenje zadane jednadžbe jednako
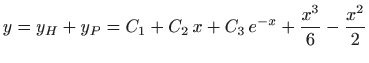
za neke konstante
pa je
Slično kao i u poglavlju 5.9.3, ako funkcija ![]() u jednadžbi (5.30) ima oblik
u jednadžbi (5.30) ima oblik
pri čemu su
Uvrštavanje u jednadžbu daje
Izjednačavanje koeficijenata po potencijama od
pa je partikularno rješenje jednako