☰
matematika2
MATEMATIKA 2 - ZBIRKA
MATEMATIKA 2 - ZBIRKA
NEODREĐENI INTEGRAL
- Površina ravninskog lika a)
- Površina ravninskog lika b)
- Astroida
- Bernoullijeva lemniskata
- Duljina luka a)
- Rotacija parabole
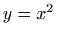
- Rotacija parabole
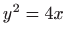
- Područje definicije funkcije
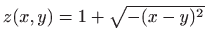
- Područje definicije funkcije
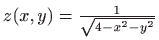
- Područje definicije funkcije
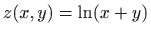
- Područje definicije funkcije
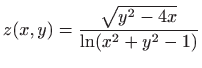
- Područje definicije funkcije

- Tangencijalna ravnina
na plohu
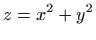 u točki
u točki
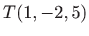
- Stožac
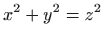 i sfera
i sfera
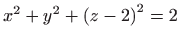 (dodiruju se
u točkama
(dodiruju se
u točkama
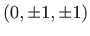 )
)
- Ploha
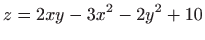
- Ploha
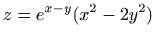
- Ploha
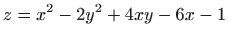 nad zatvorenim područjem
nad zatvorenim područjem
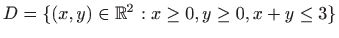 .
.
- Ploha
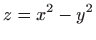 nad
zatvorenim područjem
nad
zatvorenim područjem
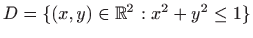 .
.
- Dio plohe
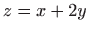 uz uvjet
uz uvjet 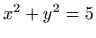 .
.
- Proizvoljni stožac upisan u kuglu polumjera
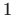 - projekcija.
- projekcija.
- Područje integracije
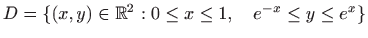 .
.
- Područje integracije
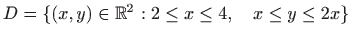 .
.
- Područje integracije
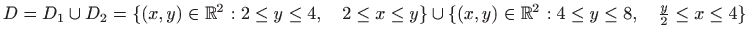 .
.
- Područje integracije
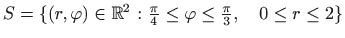 .
.
- Područje integracije
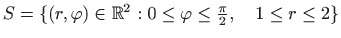 .
.
- Područje integracije
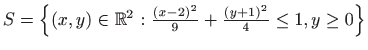 .
.
- Tijelo omeđeno plohama
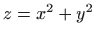 ,
, 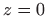 ,
, 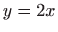 ,
, 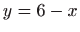 i
i 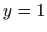 , te njegova projekcija na
, te njegova projekcija na 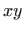 ravninu.
ravninu.
- Tijelo određeno s
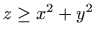 ,
,
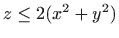 i
i 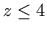 , te njegova projekcija na
, te njegova projekcija na 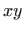 ravninu.
ravninu.
- Odsječak ravnine
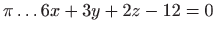 u prvom oktantu i njegova projekcija na
u prvom oktantu i njegova projekcija na 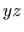 ravninu.
ravninu.
- Kugla radijusa 2 sa središtem u ishodištu, te njezina projekcija na
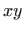 ravninu.
ravninu.
- Stožac određen sa
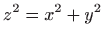 ,
,
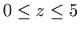 , i njegova projekcija na
, i njegova projekcija na 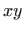 ravninu.
ravninu.
- Područje integracije zadano s
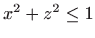 i
i
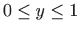 .
.
- Područje integracije
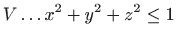 .
.
- Tijelo omeđeno paraboloidom
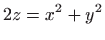 i ravninom
i ravninom
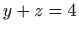 , i njegova projekcija na
, i njegova projekcija na 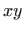 ravninu.
ravninu.
- Tijelo omeđeno sferom
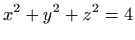 i stošcem
i stošcem
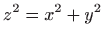 (izvan stošca).
(izvan stošca).
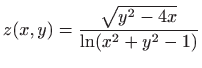
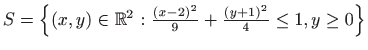 .
.
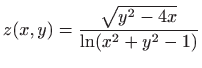
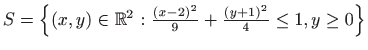 .
.